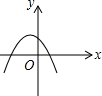题目内容
6. 长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )
长方形纸片ABCD中,E为AD边上一点,将纸片沿BE折叠后,点A落在CD边上F点,若∠CBF=∠EBF,则∠DEF的度数为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
分析 由翻折的性质可知∠ABF=∠FBE,∠AEB=∠FEB,然后由∠CBF=∠EBF可知∠ABE=30°,从而得到∠AEB=∠BEF=60°,故可求得∠DEF=60°.
解答 解:由翻折的性质可知∠ABF=∠FBE,∠AEB=∠FEB.
∵∠CBF=∠EBF,
∴∠AEB=∠FEB=∠CBF=30°.
∵∠A=∠EFB=90°,
∴∠AEB=∠BEF=60°.
∴∠DEF=180°-60°-60°=60°.
故选:D.
点评 本题主要考查的是翻折的性质,求得∠AEB=∠FEB=∠CBF=30°是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
11.抛物线y=x2+2的图象与y轴的交点坐标是( )
| A. | (-2,0) | B. | (2,0) | C. | (0,-2) | D. | (0,2) |
18.在-3,0,1,-2这四个数中,是负数的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
15.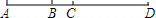 如图,点B、C在线段AD上,则下列等式中错误的是( )
如图,点B、C在线段AD上,则下列等式中错误的是( )
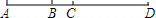 如图,点B、C在线段AD上,则下列等式中错误的是( )
如图,点B、C在线段AD上,则下列等式中错误的是( )| A. | BD-BC=AB+BC | B. | BD-BC=AD-AC | C. | AD-CD=AB+BC | D. | AD-BD=AC-BC |
16.下列计算正确的是( )
| A. | -3a-3a=00 | B. | x4-x3=x | C. | 6x3-2x3=4x3 | D. | x2+x2=x4 |
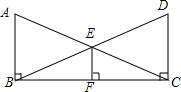 如图,已知AB⊥BC,DC⊥BC,AC与BD相交于点E,过E作EF⊥BC于点F,且AC=BD.求证:
如图,已知AB⊥BC,DC⊥BC,AC与BD相交于点E,过E作EF⊥BC于点F,且AC=BD.求证:

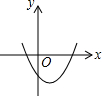
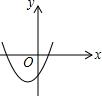
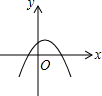
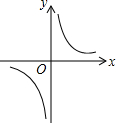 已知反比例函数y=$\frac{ab}{x}$(ab≠0)的图象如图所示,则二次函数y=ax2+bx-2的大致图象是( )
已知反比例函数y=$\frac{ab}{x}$(ab≠0)的图象如图所示,则二次函数y=ax2+bx-2的大致图象是( )