题目内容
20. 如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?
分析 (1)先由对角线互相平分证明四边形ABCD是平行四边形,再由对角互补得出∠ABC=90°,即可得出结论;
(2)先求出∠FDC=36°,再求出∠DCO=54°,然后求出∠ODC=54°,即可求出∠BDF.
解答 (1)证明:∵AO=CO,BO=DO
∴四边形ABCD是平行四边形,
∴∠ABC=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADC=90°,
∴四边形ABCD是矩形;
(2)解:∵∠ADC=90°,∠ADF:∠FDC=3:2,
∴∠FDC=36°,
∵DF⊥AC,
∴∠DCO=90°-36°=54°,
∵四边形ABCD是矩形,
∴OC=OD,
∴∠ODC=54°
∴∠BDF=∠ODC-∠FDC=18°.
点评 本题考查了矩形的判定与性质、平行四边形的判定、等腰三角形的判定与性质;熟练掌握矩形的判定与性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.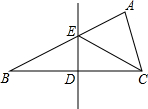 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )| A. | 1 | B. | 1+$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
15.下列事件是随机事件的是( )
| A. | 没有水分,种子发芽 | B. | 367人中至少有2人的生日相同 | ||
| C. | 三角形的内角和是180° | D. | 小华一出门上学,天就下雨 |
12.现有四把钥匙去开一把锁,其中只有二把钥匙能开这把锁,一个人随机拿其中一把钥匙开锁,若不能开则把这把钥匙扔掉,则这个人用这四把钥匙到第三次才能打开这把锁的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{5}$ |
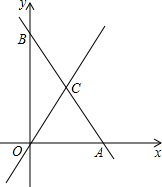 在平面直角坐标系中,直线AB的解析式为y=-2x+12,点C是线段AB的中点.
在平面直角坐标系中,直线AB的解析式为y=-2x+12,点C是线段AB的中点.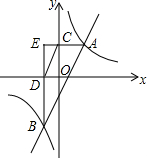 如图,反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,过点A作AC⊥y轴与点C,过点B作BD⊥x轴于点D.
如图,反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,过点A作AC⊥y轴与点C,过点B作BD⊥x轴于点D.