题目内容
2．已知二次函数y=x2+（b+1）x+c，若点A（2，c），B（m，y1），C（3，y2）在这个函数图象上，且y1＜y2，则实数m的取值范围是-1＜m＜3．分析 根据二次函数的对称性求得对称轴，然后根据函数的单调性解答．
解答 解：由二次函数y=x2+（b+1）x+c可知与y轴的交点为（0，c），
∵点A（2，c），
∴对称轴为x=1，
∴C（3，y2）的对称点为（-1，y2），
∵B（m，y1），C（3，y2）为其图象上的两点，且y1＜y2，
∴即-1＜m＜3．
故答案为-1＜m＜3．
点评 本题考查了二次函数图象上点的坐标特征．二次函数的对称性和二次函数的性质是关键．
练习册系列答案
相关题目
13．
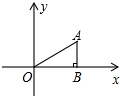如图，在平面直角坐标系xOy中，点B在x轴的正半轴上，OB=$\sqrt{3}$，AB⊥OB，∠AOB=30°．把△ABO绕点O逆时针旋转150°后得到△A1B1O，则点A的对应点A1的坐标为（ ）
如图，在平面直角坐标系xOy中，点B在x轴的正半轴上，OB=$\sqrt{3}$，AB⊥OB，∠AOB=30°．把△ABO绕点O逆时针旋转150°后得到△A1B1O，则点A的对应点A1的坐标为（ ）| A． | （0，-2） | B． | （-2，0） | C． | （-1，$-\sqrt{3}$） | D． | （$-\sqrt{3}$，-1） |
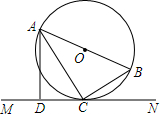如图，AB是⊙O的直径，C是⊙O上一点，直线MN经过点C，过点A作直线MN的垂线，垂足为点D，且AC平分∠BAD．