题目内容
11.(1)计算:$\sqrt{18}$-$\frac{2}{\sqrt{2}}$+|1-$\sqrt{2}$|+($\frac{1}{2}$)-1(2)化简:$\sqrt{18}$-$\sqrt{\frac{9}{2}}$-$\frac{\sqrt{3}+\sqrt{6}}{\sqrt{3}}$+($\sqrt{3}$-2)0+$\sqrt{(1-\sqrt{2})^{2}}$.
分析 (1)首先化简二次根式,去掉绝对值符号,计算负指数次幂,然后合并同类二次根式即可求解;
(2)首先化简二次根式,去掉绝对值符号,计算负指数次幂,然后合并同类二次根式即可求解.
解答 解:(1)原式=3$\sqrt{2}$-$\sqrt{2}$+($\sqrt{2}$-1)+2=3$\sqrt{2}$+1;
(2)原式=3$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$-(1+$\sqrt{2}$)+1+($\sqrt{2}$-1)
=3$\sqrt{3}$-$\frac{3\sqrt{2}}{2}$-1-$\sqrt{2}$+1+$\sqrt{2}$-1
=$\frac{3\sqrt{2}}{2}$-1.
点评 本题考查了二次根式的混合运算,以及0次幂和负指数次幂,正确对二次根式进行化简是关键.

练习册系列答案
相关题目
6.下列运算正确的是( )
| A. | $\sqrt{25}$=±5 | B. | 4$\sqrt{3}$-$\sqrt{27}$=1 | C. | $\sqrt{24}$•$\sqrt{\frac{3}{2}}$=6 | D. | $\sqrt{18}$÷$\sqrt{2}$=9 |
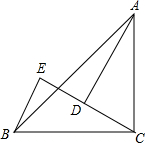 如图,在△ABC中,已知∠ACB=90°,CA=CB,AD⊥CE于点D,BE⊥CE于点E.
如图,在△ABC中,已知∠ACB=90°,CA=CB,AD⊥CE于点D,BE⊥CE于点E.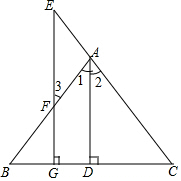 如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试说明∠1=∠2的理由.
如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试说明∠1=∠2的理由.