题目内容
13.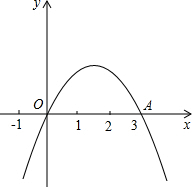 如图,二次函数y=ax2+bx+c(a≠0)的图象过原点O与点A(3,0).
如图,二次函数y=ax2+bx+c(a≠0)的图象过原点O与点A(3,0).(1)判断b的符号,并求出c的值和该二次函数图象的顶点的横坐标;
(2)若M(m,y1),N(m+n,y2)(n>0)是该二次函数图象上的两点,当y1=y2时,求m,n之间的数量关系.
分析 (1)根据图象过原点O与点A(3,0)求出对称轴判断b的符号,求出c的值和顶点的横坐标;
(2)根据y1=y2可知点M、N关于对称轴对称,得到答案.
解答 解:(1)根据图象过原点O与点A(3,0)可知,
c=0,对称轴为直线x=$\frac{3}{2}$,即-$\frac{b}{2a}$=$\frac{3}{2}$,
∵开口向下,
∴a<0,
∴b>0,
∵对称轴为直线x=$\frac{3}{2}$,
∴顶点的横坐标为$\frac{3}{2}$;
(2)∵M(m,y1),N(m+n,y2)(n>0)是该二次函数图象上的两点,且y1=y2,
∴点M、N关于对称轴对称,$\frac{m+m+n}{2}$=$\frac{3}{2}$,
∴2m+n=3.
点评 本题考查的是二次函数的性质,掌握抛物线的对称性是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
5.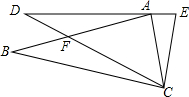 如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
 如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )
如图,在△ABC中,点F在边AB上,EC=AC,CF,EA的延长线交于点D,且∠BCD=∠ACE=∠DAB,则DE等于( )| A. | DC | B. | BC | C. | AB | D. | AE+AC |
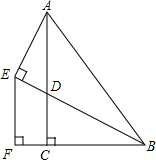 如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,连接BD,过A作AE⊥BD交BD的延长线于E,过E作EF⊥BC交BC的延长线于F,且AC=BF,BE=2AE.
如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,连接BD,过A作AE⊥BD交BD的延长线于E,过E作EF⊥BC交BC的延长线于F,且AC=BF,BE=2AE.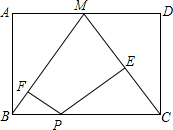 如图,点M是矩形ABCD的边AD的中点,点P是BC边上的一个动点,PE⊥CM,PF⊥BM,垂足分别E,F.
如图,点M是矩形ABCD的边AD的中点,点P是BC边上的一个动点,PE⊥CM,PF⊥BM,垂足分别E,F.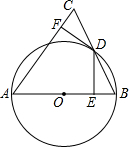 如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,以AB边为直径作⊙O,交BC边于点D,BD=DC,过点D作DE⊥AB于点E,DF⊥AC于点F.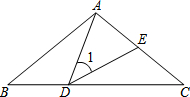 如图,△ABC中,AB=AC=5,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
如图,△ABC中,AB=AC=5,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.