题目内容
18．
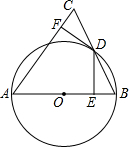如图，在△ABC中，以AB边为直径作⊙O，交BC边于点D，BD=DC，过点D作DE⊥AB于点E，DF⊥AC于点F．（1）求证：BE=CF；
（2）若⊙O的半径为5，BC=12，求DE的长．
分析 （1）如图，连接AD．通过证明Rt△BED≌Rt△CFD证得BE=CF；
（2）利用射影定理来求DE的长度．
解答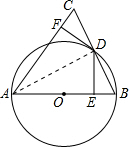 
（1）证明：如图，连接AD．
∵AB是直径，
∴AD⊥BC．
又∵BD=DC，即点D是BC的中点，
∴AD是∠CAB的平分线，
∵DE⊥AB，DF⊥AC，
∴DE=DF．
在Rt△BED与Rt△CFD中，
$\left\{\begin{array}{l}{DE=DF}\\{BE=CD}\end{array}\right.$，
∴Rt△BED≌Rt△CFD（HL），
∴BE=CF；
（2）∵⊙O的半径为5，BC=12，
∴AB=10，BD=$\frac{1}{2}$BC=6．
在直角△BDE中，DE⊥AB，
∴BD2=BE•AB，即36=10BE，
解得 BE=3.6．
又DE2=BE•AB，
∴DE2=3.6×（10-3.6），则DE=4.8．
点评 本题考查了角平分线的性质、等腰三角形的判定与性质以及圆周角定理．解答（2）题时，也可以利用勾股定理和面积法来求线段DE的长度．
练习册系列答案
相关题目
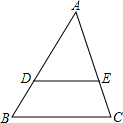在△ABC中，点D、E分别在边AB、AC上，DE∥BC，DE=3，BC=9．
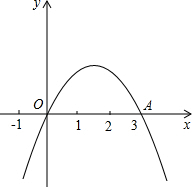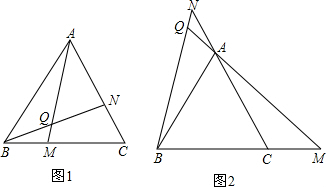
如图，二次函数y=ax2+bx+c（a≠0）的图象过原点O与点A（3，0）．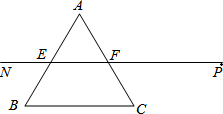
射线PN与等边△ABC的两边AB，BC分别交于点E，F，且BC∥EF，AE=BE=2cm，PF=4cm．动点Q从点P出发，沿射线PN以每秒2cm的速度向左移动，同时△ABC也沿射线PN以每秒1cm的速度向左移动，经过t秒，以点Q为圆心，$\sqrt{3}$cm为半径的圆与△ABC的边相切（切点在边上），请写出t可取的一切值t=2或3≤t≤7或t=8．（单位：秒）
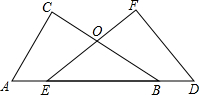如图，已知AC⊥BC，DF⊥EF，BC 与EF交于O，AC=DF，AE=BD