题目内容
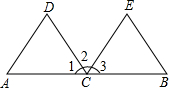
2.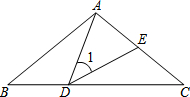 如图,△ABC中,AB=AC=5,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.
如图,△ABC中,AB=AC=5,∠BAC=100°,点D在线段BC上运动(不与点B、C重合),连接AD,作∠1=∠C,DE交线段AC于点E.(1)若∠BAD=20°,求∠EDC的度数;
(2)当DC等于多少时,△ABD≌△DCE?试说明理由;
(3)△ADE能成为等腰三角形吗?若能,请直接写出此时∠BAD的度数;
若不能,请说明理由.
分析 (1)利用三角形的外角的性质得出答案即可;
(2)利用∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC得出∠BAD=∠EDC,进而求出△ABD≌△DCE;
(3)根据等腰三角形的判定以及分类讨论得出即可.
解答 解(1)∵AB=AC,
∴∠B=∠C=$\frac{1}{2}$(180°-∠BAC)=40°,
∵∠1=∠C,
∴∠1=∠B=40°,
∵∠ADC=∠B+∠BAD,∠ADC=∠1+∠EDC.
∴∠EDC=∠BAD=20°
(2)当DC=5时,△ABD≌△DCE;
理由:∵∠ADE=40°,∠B=40°,
又∵∠ADC=∠B+∠BAD,∠ADC=∠ADE+∠EDC.
∴∠BAD=∠EDC.
在△ABD和△DCE中,
$\left\{\begin{array}{l}{∠B=∠C}\\{AB=CD}\\{∠BAD=∠EDC}\end{array}\right.$,
∴△ABD≌△DCE(ASA);
(3)当∠BAD=30°时,
∵∠B=∠C=40°,
∴∠BAC=100°,
∵∠ADE=40°,∠BAD=30°,
∴∠DAE=70°,
∴∠AED=180°-40°-70°=70°,
∴DA=DE,这时△ADE为等腰三角形;
当∠BAD=60°时,∵∠B=∠C=40°,
∴∠BAC=100°,
∵∠ADE=40°,∠BAD=60°,∠DAE=40°,
∴EA=ED,这时△ADE为等腰三角形.
点评 此题主要考查了全等三角形的判定与性质和三角形内角和定理以及等腰三角形的性质等知识,根据已知得出△ABD≌△DCE是解题关键.

练习册系列答案
相关题目
17. 某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图
某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图
(1)直接写出a、b、c的值,并补全条形统计图.
(2)这次抽样调查的数据中,中位数在哪个分数段.
(3)已知本次竞赛中有5人获得满分,其中有三名女职工,两名男职工.请用树状图或列表的方法求“从这五位满分获得者中随机抽取两人刚好是一男一女”的概率.
 某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图
某单位为增强职工的安全意识,举办了安全应急知识竞赛活动,为了解情况,从中抽取部分职工的竞赛成绩(分数为正整数)进行统计,整理成下面的表格和统计图| 成绩(分) | 49.5-59.5 | 59.5-69.5 | 69.5-79.5 | 79.5-89.5 | 89.5-100.5 |
| 频数(人) | 20 | 32 | a | b | c |
| 频率 | 0.08 | 0.20 | 0.36 |
(2)这次抽样调查的数据中,中位数在哪个分数段.
(3)已知本次竞赛中有5人获得满分,其中有三名女职工,两名男职工.请用树状图或列表的方法求“从这五位满分获得者中随机抽取两人刚好是一男一女”的概率.
11.计算:-1-2=( )
| A. | 1 | B. | -1 | C. | -2 | D. | -3 |
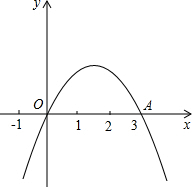 如图,二次函数y=ax2+bx+c(a≠0)的图象过原点O与点A(3,0).
如图,二次函数y=ax2+bx+c(a≠0)的图象过原点O与点A(3,0).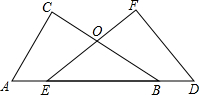 如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD
如图,已知AC⊥BC,DF⊥EF,BC 与EF交于O,AC=DF,AE=BD
 如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE.
如图,点C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE. 如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求:
如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=3,AC=$\sqrt{10}$,求: