题目内容
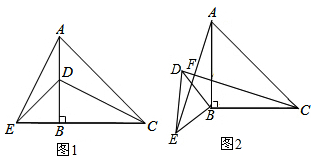
6.(1)如图1,△ABC和△E中,AB=CB,DB=EB,∠ABC=∠DBE=90°,D点在AB上,连接AE、DC.则AE和CD有什么数量和位置关系?(2)类比:
若将图1中的△DBE绕点B逆时针旋转一个锐角,如图2所示,问图2中的线段AE,CD之间的数量和位置关系还成立吗?若成立,请给予证明;若不成立,请说明理由.
分析 (1)延长CD交AE于K,根据全等三角形的性质得到AE=CD,∠EAB=∠DCB,由于∠DCB+∠CDB=90°,于是得到结论;
(2)由于∠DBE=∠ABC=90°,得到∠ABE=∠DBC,根据全等三角形的性质得到AE=CD,∠EAB=∠DCB,等量代换得到∠KOA+∠KAO=90°,于是得到结论.
解答  解:(1)AE=CD,AE⊥CD,
解:(1)AE=CD,AE⊥CD,
理由:延长CD交AE于F,
在△AEB和△CDB中,
∵$\left\{\begin{array}{l}{∠ABE=∠CBD=90°}\\{AB=BC}\\{BE=DB}\end{array}\right.$,
∴△AEB≌△CDB(SAS)
∴AE=CD,
∠EAB=∠DCB,
∵∠DCB+∠CDB=90°,
∠ADF=∠CDB,
∴∠ADF+∠DAF=90°,
∴∠AFD=90°,
∴AE⊥CD;
(2)解:(2)AE=CD,AE⊥CD,
∵∠DBE=∠ABC=90°,
∴∠ABE=∠DBC,
在△AEB和△CDB中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠DBC}\\{BE=BD}\end{array}\right.$
∴△AEB≌△CDB,
∴AE=CD,∠EAB=∠DCB,
∵∠DCB+∠COB=90°,∠AOK=∠COB,
∴∠KOA+∠KAO=90°,
∴∠AKC=90°,
∴AE⊥CD.
点评 此题考查了全等三角形的判定与性质,用到的知识点全等三角形的判定与性质,关键是能在较复杂的图形中找出全等的三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.某小学为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
| A. | 平均数是15 | B. | 众数是10 | C. | 中位数是17 | D. | 方差是$\frac{44}{3}$ |
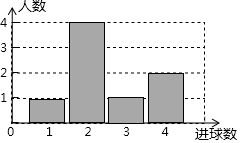 体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示. 如图,AB=AC,BD=CE,用无刻度的直尺画出∠A的平分线.
如图,AB=AC,BD=CE,用无刻度的直尺画出∠A的平分线.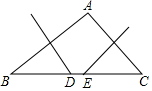 如图,△ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是10cm.
如图,△ABC中,BC=10cm,AB的中垂线交于BC于D,AC的中垂线交BC于E,则△ADE的周长是10cm.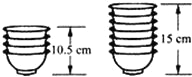 如图,两摞规格相同的碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题:
如图,两摞规格相同的碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题: