题目内容
⊙O的半径为6,一条弦长为6,则圆心到这条弦的距离= ,这条弦所对的圆周角= 度.
考点:圆周角定理,等边三角形的判定与性质
专题:
分析:根据⊙O的一条弦长恰好等于半径知:这条弦和两条半径组成了等边三角形.所以这条弦所对的圆心角是60°,再根据弦所对的圆周角有两种情况讨论求解,根据三角函数可求出圆心到这条弦的距离.
解答: 解:如图所示:
解:如图所示:
∵AO=AB=6,
∴△OAB是等边三角形,
∴∠A=60°,
过O作OC⊥AB,
∴CO=AO×sinA=6×
=3
;
①当圆周角的顶点在优弧上时,则圆周角=
×60°=30°;
②当圆周角的顶点在劣弧上时,则根据圆内接四边形的性质,和第一种情况的圆周角是互补,等于150°.
故答案为:3
;30或150.
 解:如图所示:
解:如图所示:∵AO=AB=6,
∴△OAB是等边三角形,
∴∠A=60°,
过O作OC⊥AB,
∴CO=AO×sinA=6×
| ||
| 2 |
| 3 |
①当圆周角的顶点在优弧上时,则圆周角=
| 1 |
| 2 |
②当圆周角的顶点在劣弧上时,则根据圆内接四边形的性质,和第一种情况的圆周角是互补,等于150°.
故答案为:3
| 3 |
点评:此题主要考查了圆周角定理,等边三角形的判定和性质,关键是要注意:一条弦所对的圆周角有两种情况,且两种情况的角是互补的关系.

练习册系列答案
相关题目
已知圆锥的母线长是35,它的侧面展开图是圆心角为216°的扇形,那么这个圆锥的( )
| A、底面半径是15 |
| B、高是26 |
| C、侧面积是700π |
| D、底面积是441π |
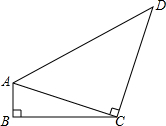 如图,四边形ABCD中,∠B=90°,AB=1,CD=8,AC⊥CD,若sin∠ACB=
如图,四边形ABCD中,∠B=90°,AB=1,CD=8,AC⊥CD,若sin∠ACB=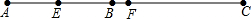 线段AB和AC在一条直线上,若E为AB的中点,F为AC的中点.
线段AB和AC在一条直线上,若E为AB的中点,F为AC的中点. 如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D.
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D.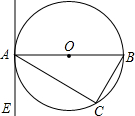 如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAE=∠B.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAE=∠B.