题目内容
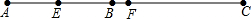 线段AB和AC在一条直线上,若E为AB的中点,F为AC的中点.
线段AB和AC在一条直线上,若E为AB的中点,F为AC的中点.(1)如果AB=6cm,AC=10cm,求EF的长;
(2)如果BC=16cm,求EF的长.
考点:两点间的距离
专题:
分析:(1)如图(1),由E为AB的中点,F为AC的中点,可得AE=
AB=3cm,AF=
AC=5cm,所以EF=AF-AE=5-3=2cm;
(2)如图(2),由E为AB的中点,F为AC的中点,可得AE=
AB,AF=
AC,设AE=BE=x,BF=y,则CF=AF=2x+y,所以BC=2x+2y=16,可得x+y=8,因为EF=x+y,所以EF=8cm.
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图(2),由E为AB的中点,F为AC的中点,可得AE=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)如图(1)

∵E为AB的中点,F为AC的中点,
∴AE=
AB=3cm,AF=
AC=5cm,
∴EF=AF-AE=5-3=2cm;
(2)如图(2),

∵E为AB的中点,F为AC的中点,
∴AE=
AB,AF=
AC,
设AE=BE=x,BF=y,则CF=AF=2x+y,
∴BC=2x+2y=16,
∴x+y=8,
∵EF=x+y,
∴EF=8cm.

∵E为AB的中点,F为AC的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=AF-AE=5-3=2cm;
(2)如图(2),

∵E为AB的中点,F为AC的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
设AE=BE=x,BF=y,则CF=AF=2x+y,
∴BC=2x+2y=16,
∴x+y=8,
∵EF=x+y,
∴EF=8cm.
点评:此题考查了两点间的距离,解题的关键是:利用中点的性质解题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
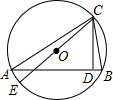 如图,已知⊙O为△ABC的外接圆,CE是⊙O的直径,CD⊥AB,D为垂足,求证:∠ACD=∠BCE.
如图,已知⊙O为△ABC的外接圆,CE是⊙O的直径,CD⊥AB,D为垂足,求证:∠ACD=∠BCE.