题目内容
 如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D.
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D.(1)求BC,AD的长度;
(2)求点O到弦BD的距离.
考点:圆周角定理,勾股定理,等腰直角三角形
专题:
分析:(1)首先根据圆周角定理可得∠ACB=90°,∠ADB=90°,∠ACD=∠BCD再利用勾股定理计算出BC,AD的长即可;
(2)过O作EO⊥DB,根据三角函数可得EO=BO×sin45°,代入响应数值可得答案.
(2)过O作EO⊥DB,根据三角函数可得EO=BO×sin45°,代入响应数值可得答案.
解答:解:(1)∵AB是直径,
∴∠ACB=90°,∠ADB=90°,
∵AB=10cm,AC=6cm,
∴BC=
=8(cm),
∵∠ACB的平分线交⊙O于D,
∴∠ACD=∠BCD,
∴AD=BD,
∵∠ADB=90°,
∴AD2+BD2=AD2,
∴AD2+AD2=102,
AD=5
cm;

(2)过O作EO⊥DB,
∵AD=BD,
∴∠ABD=45°,
∴EO=BO×sin45°=
AB•sin45°=
,
∴点O到弦BD的距离为
.
∴∠ACB=90°,∠ADB=90°,
∵AB=10cm,AC=6cm,
∴BC=
| 102-62 |
∵∠ACB的平分线交⊙O于D,
∴∠ACD=∠BCD,
∴AD=BD,
∵∠ADB=90°,
∴AD2+BD2=AD2,
∴AD2+AD2=102,
AD=5
| 2 |

(2)过O作EO⊥DB,
∵AD=BD,
∴∠ABD=45°,
∴EO=BO×sin45°=
| 1 |
| 2 |
5
| ||
| 2 |
∴点O到弦BD的距离为
5
| ||
| 2 |
点评:此题主要考查了圆周角定理,以及勾股定理的应用,关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
将含盐m%的盐水100g制成含盐2m%的盐水时,要加盐( )
A、
| ||
B、
| ||
C、
| ||
D、
|
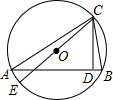 如图,已知⊙O为△ABC的外接圆,CE是⊙O的直径,CD⊥AB,D为垂足,求证:∠ACD=∠BCE.
如图,已知⊙O为△ABC的外接圆,CE是⊙O的直径,CD⊥AB,D为垂足,求证:∠ACD=∠BCE. 如图,△ABC中,AB=6,AC=8,BC=10,
如图,△ABC中,AB=6,AC=8,BC=10,