题目内容
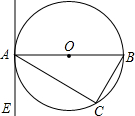 如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAE=∠B.
如图,△ABC内接于⊙O,AB为⊙O的直径,∠CAE=∠B.(1)当AB是直径时,AE是⊙O的切线吗?说明理由;
(2)当AB不是直径时,AE是⊙O的切线这个结论还成立吗?试说明你的理由.
考点:切线的判定
专题:
分析:(1)因为直线DE经过圆上A点,所以欲证AE是切线,只需证明DE⊥AB,即证∠EAB=90°即可.根据直径所对的圆周角是直角代换后可证;
(2)连接AO并延长交圆于点F,连接FC,构造(1)的图形,运用相同思路可证是切线.
(2)连接AO并延长交圆于点F,连接FC,构造(1)的图形,运用相同思路可证是切线.
解答: (1)解:AE是⊙O的切线,
(1)解:AE是⊙O的切线,
理由是:如图1,∵AB是直径,
∴∠ACB=90°,
∴∠B+∠CAB=90°,
∵∠EAC=∠B,
∴∠EAC+∠CAB=90°,
即∠EAB=90°,
∴AE是⊙O的切线;
(2)解:AE还是切线,理由如下:
如图2,连接AO并延长交圆于点F,连接FC,
∵∠B=∠F,∠CAE=∠B,
∴∠CAE=∠F.
根据(1)的证明可知,AE是⊙O的切线.
 (1)解:AE是⊙O的切线,
(1)解:AE是⊙O的切线,理由是:如图1,∵AB是直径,
∴∠ACB=90°,
∴∠B+∠CAB=90°,
∵∠EAC=∠B,
∴∠EAC+∠CAB=90°,
即∠EAB=90°,
∴AE是⊙O的切线;
(2)解:AE还是切线,理由如下:
如图2,连接AO并延长交圆于点F,连接FC,
∵∠B=∠F,∠CAE=∠B,
∴∠CAE=∠F.
根据(1)的证明可知,AE是⊙O的切线.
点评:此题考查切线的判定及圆周角定理等知识点,本题考查了学生的推理能力,题目比较典型,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
将含盐m%的盐水100g制成含盐2m%的盐水时,要加盐( )
A、
| ||
B、
| ||
C、
| ||
D、
|
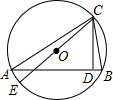 如图,已知⊙O为△ABC的外接圆,CE是⊙O的直径,CD⊥AB,D为垂足,求证:∠ACD=∠BCE.
如图,已知⊙O为△ABC的外接圆,CE是⊙O的直径,CD⊥AB,D为垂足,求证:∠ACD=∠BCE.