Question

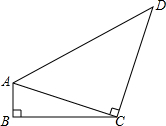如图，四边形ABCD中，∠B=90°，AB=1，CD=8，AC⊥CD，若sin∠ACB=

1

6

，则cos∠ADC=

 

．

Answer 1

考点：解直角三角形

专题：

分析：首先在△ABC中，根据三角函数值计算出AC的长，再利用勾股定理计算出AD的长，然后根据余弦定义可算出cos∠ADC．

解答：解：∵∠B=90°，sin∠ACB=

1

6

，
∴

AB

AC

=

1

6

，
∵AB=1，
∴AC=6，
∵AC⊥CD，
∴∠ACD=90°，
∴AD=

AC2+CD2

=

36+64

=10，
∴cos∠ADC=

DC

AD

=

4

5

．
故答案为：

4

5

．

点评：本题考查了解直角三角形，以及勾股定理的应用，关键是利用三角函数值计算出AC的长，再利用勾股定理计算出AD的长．