题目内容
13.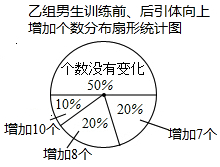 某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.
某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.甲组男生训练前、后引体向上个数统计表(单位:个)
| 甲组 | 男生A | 男生B | 男生C | 男生D | 男生E | 男生F | 平均个数 | 众数 | 中位数 |
| 训练前 | 4 | 6 | 4 | 3 | 5 | 2 | 4 | b | 4 |
| 训练后 | 8 | 9 | 6 | 6 | 7 | 6 | a | 6 | c |
(1)a=7,b=4,c=6.5;
(2)甲组训练后引体向上的平均个数比训练前增长了75%;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占到该组人数的50%,所以乙组的平均个数不可能提高4个之多.:你同意他的观点吗?说明理由.
分析 (1)根据平均数、众数和中位数的定义即可求解;
(2)根据$\frac{增长量}{原来的数值}$即可求得增长率;
(2)求出各组的增长的数值,即可作出判断;
(3)设第二组的人数是x,判断二组增长的数值是否是9x-6x即可.
解答 解:(1)a=(8+9+6+6+7+6)÷6=7,
b=4,
c=(6+7)÷2=6.5;
(2)(7-4)÷4×100%
=3÷4×100%
=75%;
(3)甲组训练效果较好.
因为甲组训练后的平均个数比训练前增长75%,
乙组训练后的平均个数比训练前增长约67%,
甲组训练前、后平均个数的增长率大于乙组的增长率.
(4)不同意.
因为乙组训练后的平均个数增加了:
50%×0+20%×7+20%×8+10%×10=4个,
所以不同意小华的观点.
故答案为:7,4,6.5;75.
点评 本题考查了统计表,扇形统计图和条形统计图,正确判断小华的观点的正误是本题的难点.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
3.在平面直角坐标系中,A(1,$\sqrt{3}$),点O为坐标原点,则线段OA的长为( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{10}$ | D. | 4 |
1.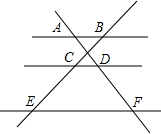 如图,已知AB∥CD∥EF,那么下列结论中正确的是( )
如图,已知AB∥CD∥EF,那么下列结论中正确的是( )
 如图,已知AB∥CD∥EF,那么下列结论中正确的是( )
如图,已知AB∥CD∥EF,那么下列结论中正确的是( )| A. | $\frac{CD}{EF}$=$\frac{AD}{AF}$ | B. | $\frac{AB}{CD}$=$\frac{BC}{EC}$ | C. | $\frac{AD}{BC}$=$\frac{AF}{BE}$ | D. | $\frac{CE}{BE}$=$\frac{AF}{AD}$ |
8.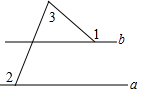 如图,已知直线a∥b,则∠1+∠2-∠3=( )
如图,已知直线a∥b,则∠1+∠2-∠3=( )
 如图,已知直线a∥b,则∠1+∠2-∠3=( )
如图,已知直线a∥b,则∠1+∠2-∠3=( )| A. | 180° | B. | 150° | C. | 135° | D. | 90° |
18.以下说法正确的是( )
| A. | 若$\sqrt{x-1}$+$\sqrt{1-x}$=y+4,则xy的平方根为1 | B. | 3-2$\sqrt{2}$的绝对值是2$\sqrt{2}$-3 | ||
| C. | 若$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$成立,则a≤0且b≥0 | D. | 若$\sqrt{(1-a)^{2}}$+$\sqrt{(a-3)^{2}}$=2,则a≥3 |
5.九年级数学兴趣小组经过市场调查,得到某种图书每月的销售与售价的关系为函数关系如下表:
已知该图书的进价为每本30元,设售价为x元.
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价(元/本) | 50 | 55 | 60 | 65 | … |
| 月销量(本) | 2000 | 1800 | 1600 | 1400 | … |
(1)请用含x的式子表示:①销售该图书每本的利润是x-30元,②月销量是-40x+4000件.(用x表示直接写出结果)
(2)若销售图书的月利润为48000元,则每本图书需要售价多少元?
(3)设销售该图书的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?