题目内容
4.计算:(1)计算:-12+(-2)3×$\frac{1}{8}$-$\root{3}{-27}$×(-$\sqrt{\frac{1}{9}}$)
(2)计算:(2+1)(22+1)(24+1)…(2128+1)+1.
(3)先化简,再求值:[(x+2y)(x-2y)-(x+4y)2]÷4y,其中x=5,y=2.
分析 (1)原式先计算乘方及立方根定义,再计算乘法运算,最后算加减运算即可得到结果;
(2)原式变形后,利用平方差公式计算即可得到结果;
(3)原式中括号中利用平方差公式及完全平方公式化简,去括号合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
解答 解:(1)原式=-1-8×$\frac{1}{8}$-(-3)×(-$\frac{1}{3}$)=-1-1-1=-3;
(2)原式=(2-1)(2+1)(22+1)(24+1)…(2128+1)+1
=(22-1)(22+1)(24+1)…(2128+1)+1
=(24-1)(24+1)…(2128+1)+1
=…
=2256-1+1
=2256;
(3)原式=(x2-4y2-x2-8xy-16y2)÷4y
=-2x-5y,
当x=5,y=2时,原式=-10-10=-20.
点评 此题考查了整式的混合运算-化简求值,以及实数的运算,熟练掌握运算法则及公式是解本题的关键.

练习册系列答案
相关题目
14.下列各式计算正确的是( )
| A. | (-2$\sqrt{3}$)2=6 | B. | $\sqrt{1\frac{25}{49}}$=1$\frac{5}{7}$ | ||
| C. | $\sqrt{(-121)×(-9)}$=$\sqrt{121}$×$\sqrt{9}$=33 | D. | $\sqrt{(-4)^{2}}$=±4 |
12.下列说法正确的是( )
| A. | 最小的有理数是0 | |
| B. | 任何有理数都可以用数轴上的点表示 | |
| C. | 绝对值等于它的相反数的数都是负数 | |
| D. | 整数是正整数和负整数的统称 |
19.下列式子中,正确的是( )
| A. | -$\sqrt{3.6}$=-0.6 | B. | $\sqrt{36}$=±6 | C. | $\sqrt{(-13)^{2}}$=-13 | D. | $\root{3}{-5}$=-$\root{3}{5}$ |
13.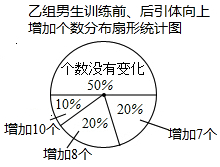 某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.
某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.
甲组男生训练前、后引体向上个数统计表(单位:个)
(1)根据以上信息,解答下列问题:
(1)a=7,b=4,c=6.5;
(2)甲组训练后引体向上的平均个数比训练前增长了75%;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占到该组人数的50%,所以乙组的平均个数不可能提高4个之多.:你同意他的观点吗?说明理由.
 某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.
某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有6名男生,并对两组男生训练前,后引体向上的个数进行统计分析,得到乙组男生训练前,后引体向上的平均个数分别是6个和10个,及下面不完整的统计表和图的统计图.甲组男生训练前、后引体向上个数统计表(单位:个)
| 甲组 | 男生A | 男生B | 男生C | 男生D | 男生E | 男生F | 平均个数 | 众数 | 中位数 |
| 训练前 | 4 | 6 | 4 | 3 | 5 | 2 | 4 | b | 4 |
| 训练后 | 8 | 9 | 6 | 6 | 7 | 6 | a | 6 | c |
(1)a=7,b=4,c=6.5;
(2)甲组训练后引体向上的平均个数比训练前增长了75%;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占到该组人数的50%,所以乙组的平均个数不可能提高4个之多.:你同意他的观点吗?说明理由.

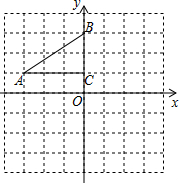 如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(-3,1),B(0,3),C(0,1)
如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(-3,1),B(0,3),C(0,1)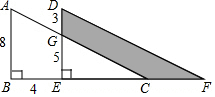 如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.求图中阴影部分的面积.
如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF.求图中阴影部分的面积.