题目内容
20．
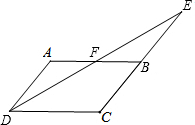如图，四边形ABCD中，AD∥BC，F是AB的中点，DF交CB延长线于E，CE=CD．求证：∠ADE=∠EDC．
分析 先根据平行线的性质，得出∠ADE=∠E，再根据等边对等角，得出∠EDC=∠E，最后根据等量代换，得出∠ADE=∠EDC．
解答 证明：∵AD∥BC，
∴∠ADE=∠E，
又∵CE=CD，
∴∠EDC=∠E，
∴∠ADE=∠EDC．
点评 本题主要考查了平行线的性质以及等腰三角形的性质，解题时注意：两条平行线被第三条直线所截，内错角相等． 简单说成：两直线平行，内错角相等．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
补全解题过程．
如图，两条交叉的公路上分别有A、B两个车站，要在这两条公路之间修一个储运仓库，使它到两条公路的距离相等，且又要到两个车站的距离相等，请你在图中画出这个储运仓库P的位置．
如图，在△ABC中，∠ACB=90°，点D，E在AB上，且AF垂直平分CD，BG垂直平分CE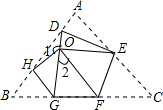
如图，将△ABC沿DE、HG、EF翻折，三个顶点均落在点O处，若∠1=142°，则∠2的度数为38°．
如图，三角形纸片ABC中∠A=63°，∠B=77°，将纸片的一角折叠，使点C落在△ABC内，如图，若∠1=50°，则∠2=30°．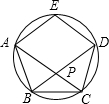
用量角器将圆五等分，得到正五边形ABCDE（如图），AC、BD相交于点P，则∠APB等于72°．