题目内容
2.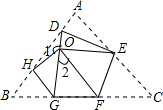 如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=142°,则∠2的度数为38°.
如图,将△ABC沿DE、HG、EF翻折,三个顶点均落在点O处,若∠1=142°,则∠2的度数为38°.
分析 先根据折叠性质得:∠HOG=∠B,∠DOE=∠A,∠EOF=∠C,根据三角形内角和为180°和周角360°求出结论.
解答 解:由折叠得:∠HOG=∠B,∠DOE=∠A,∠EOF=∠C,
∵∠A+∠B+∠C=180°,
∴∠HOG+∠DOE+∠EOF=180°,
∵∠1+∠2+∠HOG+∠DOE+∠EOF=360°,
∴∠1+∠2=180°,
∵∠1=142°,
∴∠2=180°-142°=38°,
故答案为:38°.
点评 本题是折叠问题,考查了折叠的性质,熟练掌握折叠前后的两个角相等,结合三角形的内角和求出角的度数.

练习册系列答案
相关题目
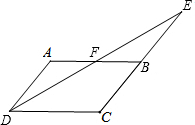 如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.
如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.