题目内容
11. 补全解题过程.
补全解题过程.如图,在△ABC中∠ABC平分线BP和外角平分线CP交于点P,试猜想∠A与∠P之间的关系,并说明理由.
解:∠A=2∠P
理由:∵BP、CP分别平分∠ABC、∠ACD(已知)
∴∠ABC=2∠1,∠ACD=2∠2 (角平分线的定义)
∵∠ACD为△ABC的外角
∴∠ACD=∠A+∠ABC=∠A+2∠1(三角形外角的性质)
即:2∠2=∠A+2∠1
同理:∠2=∠P+∠1
∴∠A=2∠P.
分析 根据角平分线的定义以及三角形的一个外角等于与它不相邻的两个内角的和分别填空即可.
解答 解:∠A=2∠P
理由:∵BP、CP分别平分∠ABC、∠ACD(已知)
∴∠ABC=2∠1,∠ACD=2∠2 (角平分线的定义)
∵∠ACD为△ABC的外角
∴∠ACD=∠A+∠ABC=∠A+2∠1(三角形外角的性质)
即:2∠2=∠A+2∠1,
同理:∠2=∠P+∠1,
∴∠A=2∠P.
故答案为:2,角平分线的定义,ABC,∠1.
点评 本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,主要是逻辑推理能力的训练.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 尺规作图:已知∠α,求作:∠A使∠A=∠α( 不写作法,保留痕迹 )
尺规作图:已知∠α,求作:∠A使∠A=∠α( 不写作法,保留痕迹 ) 求如图4×4方格中线段AE,BC,CD的长.
求如图4×4方格中线段AE,BC,CD的长.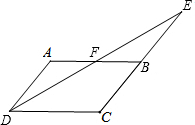 如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.
如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.