题目内容
15. 如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE
如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE(1)求∠ECD的度数;
(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示?并证明你的结论.
分析 (1)设∠ADC=x,∠BEC=y.由AF垂直平分CD,根据线段垂直平分线的性质得出AC=AD,由等边对等角得到∠ADC=∠ACD=x,同理∠BEC=∠BCE=y.在△ACD中,由三角形内角和定理得出2x+∠CAD=180°①,同理,2y+∠CBE=180°②,①+②,得2x+2y+∠CAD+∠CBE=360°③,而∠CAD+∠CBE=90°④,④代入③得出x+y=135°,再利用三角形内角和定理得出∠ECD=180°-(x+y)=45°;
(2)同(1)求解即可.
解答 解:(1)设∠ADC=x,∠BEC=y.
∵AF垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD=x,
同理∠BEC=∠BCE=y.
在△ACD中,∵∠ADC+∠ACD+∠CAD=180°,
∴2x+∠CAD=180°①,
同理,2y+∠CBE=180°②,
①+②,得2x+2y+∠CAD+∠CBE=360°③,
∵∠CAD+∠CBE+∠ACB=180°,∠ACB=90°,
∴∠CAD+∠CBE=90°④,
④代入③,得2x+2y+90°=360°,
∴x+y=135°,
∴∠ECD=180°-(x+y)=45°;
(2)由(1)可得2x+2y+∠CAD+∠CBE=360°,
∵∠CAD+∠CBE=180°-∠ACB=180°-α,
∴2x+2y+180°-α=360°,
∴x+y=90°+$\frac{1}{2}$α,
∴∠ECD=180°-(x+y)=180°-(90°+$\frac{1}{2}$α)=90°-$\frac{1}{2}$α.
点评 本题考查了线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等,也考查了等腰三角形的性质,三角形内角和定理,难度适中.

练习册系列答案
相关题目
 求如图4×4方格中线段AE,BC,CD的长.
求如图4×4方格中线段AE,BC,CD的长.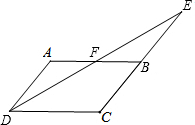 如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.
如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.