题目内容
6.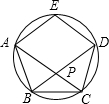 用量角器将圆五等分,得到正五边形ABCDE(如图),AC、BD相交于点P,则∠APB等于72°.
用量角器将圆五等分,得到正五边形ABCDE(如图),AC、BD相交于点P,则∠APB等于72°.
分析 首先根据正五边形的性质得到AB=BC=CD,∠ABC=∠BCD=108度,然后利用三角形内角和定理得∠BAC=∠BCA=∠CBD=∠BDC=$\frac{180°-108°}{2}$=36°,最后利用三角形的外角的性质得到∠APB=∠DBC+∠ACB=72°.
解答 解:∵五边形ABCDE为正五边形,
∴AB=BC=CD,∠ABC=∠BCD=108度,
∴∠BAC=∠BCA=∠CBD=∠BDC=$\frac{180°-108°}{2}$=36°,
∴∠APB=∠DBC+∠ACB=72°,
故答案为:72°.
点评 本题考查了正多边形和圆的知识,题目中还用到了三角形的外角的性质及正多边形的性质等,比较简单.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
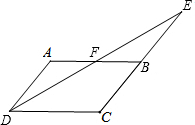 如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.
如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC. 求作一点P,使点P到∠A两边的距离相等,且点P到点D和点E的距离相等.(保留作图痕迹)
求作一点P,使点P到∠A两边的距离相等,且点P到点D和点E的距离相等.(保留作图痕迹)