题目内容
9. 如图,三角形纸片ABC中∠A=63°,∠B=77°,将纸片的一角折叠,使点C落在△ABC内,如图,若∠1=50°,则∠2=30°.
如图,三角形纸片ABC中∠A=63°,∠B=77°,将纸片的一角折叠,使点C落在△ABC内,如图,若∠1=50°,则∠2=30°.
分析 先由折叠性质得:∠C=∠C′=40°,根据三角形内角和求出∠CEC′+∠CFC′=280°,由平角定义可知:∠1+∠2+∠CFC′+∠CEC′=360°,从而得出∠2=30°.
解答  解:∵∠A=63°,∠B=77°,
解:∵∠A=63°,∠B=77°,
∴∠C=180°-∠A-∠B=180°-63°-77°=40°,
由折叠得:∠C=∠C′=40°,∠CEF=∠C′EF,∠CFE=∠C′FE,
∴∠CEC′+∠CFC′=180°+180°-40°-40°=280°,
∵∠1+∠CFC′=180°,∠2+∠CEC′=180°,
∴∠1+∠2+∠CFC′+∠CEC′=360°,
∴∠1+∠2=360°-280°=80°,
∵∠1=50°,
∴∠2=30°,
故答案为:30°.
点评 本题是折叠问题,考查了折叠的性质:折叠前后的两个角对应相等;与三角形的内角和及平角为180°求角的度数.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
19.下列说法不正确的是( )
| A. | 两点之间,线段最短 | B. | 连结两点的线段叫做这两点的距离 | ||
| C. | 两点确定一条直线 | D. | 同角的补角相等 |
 求如图4×4方格中线段AE,BC,CD的长.
求如图4×4方格中线段AE,BC,CD的长.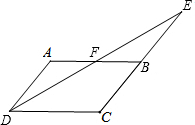 如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.
如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.