题目内容
7.求下列分式的值:(1)$\frac{{x}^{2}+2xy+{y}^{2}}{{x}^{2}-{y}^{2}}$,其中x=5,y=-10.
(2)$\frac{x}{1-x}$+$\frac{x}{1+x}$,其中,x=-3.
分析 (1)先将原式分子、分母因式分解,再约分即可化简,最后将x、y的值代入即可得;
(2)先通分化为同分母分式相加,再将x的值代入计算可得.
解答 解:(1)原式=$\frac{(x+y)^{2}}{(x+y)(x-y)}$=$\frac{x+y}{x-y}$,
当x=5、y=10时,原式=$\frac{5+10}{5-10}$=-3;
(2)原式=$\frac{x(1+x)}{(1-x)(1+x)}$+$\frac{x(1-x)}{(1-x)(1+x)}$
=$\frac{2x}{(1-x)(1+x)}$,
当x=-3时,原式=$\frac{2×(-3)}{(1+3)(1-3)}$=$\frac{3}{4}$.
点评 本题主要考查分式的化简求值,熟练掌握分数的混合运算顺序及运算法则是解题的关键.

练习册系列答案
相关题目
19.下列说法不正确的是( )
| A. | 两点之间,线段最短 | B. | 连结两点的线段叫做这两点的距离 | ||
| C. | 两点确定一条直线 | D. | 同角的补角相等 |
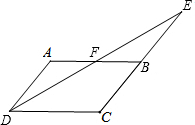 如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC.
如图,四边形ABCD中,AD∥BC,F是AB的中点,DF交CB延长线于E,CE=CD.求证:∠ADE=∠EDC. 求作一点P,使点P到∠A两边的距离相等,且点P到点D和点E的距离相等.(保留作图痕迹)
求作一点P,使点P到∠A两边的距离相等,且点P到点D和点E的距离相等.(保留作图痕迹)