题目内容
在△ABC中，∠ACB=90°，AC=6，BC=8，点D为直线AC上一点，且△ABD是等腰三角形，求△ABD的周长．
考点：等腰三角形的判定,勾股定理
专题：分类讨论
分析：分三种情况讨论，当BA=BD时，可知AD=2AC=12；当BA=AD时，两种情况当C、D在A点两侧时，CD=AD+AC=16，利用勾股定理可求得BD，当C、D在A点同侧时，则CD=4，同理求得BD；当AD=BD时，设AD=BD=x，利用勾股定理可求得x；再计算其周长即可．
解答：解：∵∠ACB=90°，AC=6，BC=8，
∴AB=10，
当BA=BD=10时，则可知AD=2AC=12，则△ABC的周长为10+10+12=32；
当BA=AD=10时，
①若C、D在点A的两侧，则CD=CA+DA=6+10=16，在Rt△BCD中，由勾股定理可得BD=
=
=8
，则△ABC的周长为：10+10+8
=20+8
，
②若C、D在点A的同侧，则CD=AD-AC=10-6=4，在Rt△BCD中，由勾股定理可得BD=
=
=4
，则△ABC的周长为：10+10+4
=20+4
，
当AD=BD时，设AD=BD=x，则CD=AD-AC=x-6，在Rt△BCD中，由勾股定理可得BD2=BC2+CD2，即x2=（x-6）2+82，解得x=
，则△ABC的周长为：10+
+
=
，
综上可知△ABC的周长为32或20+8
或20+4
或
．
∴AB=10，
当BA=BD=10时，则可知AD=2AC=12，则△ABC的周长为10+10+12=32；
当BA=AD=10时，
①若C、D在点A的两侧，则CD=CA+DA=6+10=16，在Rt△BCD中，由勾股定理可得BD=
| BC2+CD2 |
| 162+82 |
| 5 |
| 5 |
| 5 |
②若C、D在点A的同侧，则CD=AD-AC=10-6=4，在Rt△BCD中，由勾股定理可得BD=
| BC2+CD2 |
| 42+82 |
| 5 |
| 5 |
| 5 |
当AD=BD时，设AD=BD=x，则CD=AD-AC=x-6，在Rt△BCD中，由勾股定理可得BD2=BC2+CD2，即x2=（x-6）2+82，解得x=
| 25 |
| 3 |
| 25 |
| 3 |
| 25 |
| 3 |
| 80 |
| 3 |
综上可知△ABC的周长为32或20+8
| 5 |
| 5 |
| 80 |
| 3 |
点评：本题主要考查等腰三角形的性质，分三种情况确定出点D的位置是解题的关键，注意方程思想的应用．
练习册系列答案
相关题目
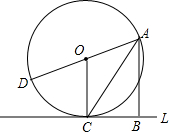如图所示，直线L切⊙O于点C，AD为⊙O的任意一条直径，点B在直线L上，且∠BAC=∠CAD（AD与AB不在一条直线上），试判断四边形ABCO为怎样的特殊四边形？