题目内容
已知抛物线y=ax2+bx+c经过P(0,-1)、Q(1,2)、M(-3,2)三点.
(1)求此抛物线的表达式;
(2)在此抛物线上求出到两坐标轴距离相等的点的坐标.
(1)求此抛物线的表达式;
(2)在此抛物线上求出到两坐标轴距离相等的点的坐标.
考点:待定系数法求二次函数解析式,二次函数图象上点的坐标特征
专题:
分析:(1)将P(0,-1)、Q(1,2)、M(-3,2)三点的坐标分别代入y=ax2+bx+c,利用待定系数法即可求出此抛物线的表达式;
(2)到两坐标轴距离相等的点的坐标满足的条件是:横坐标与纵坐标相等或者横坐标与纵坐标互为相反数,将y=x和y=-x分别代入(1)中所求的解析式,得到关于x的一元二次方程,解方程求出x的值,再得到y的值,即可求解.
(2)到两坐标轴距离相等的点的坐标满足的条件是:横坐标与纵坐标相等或者横坐标与纵坐标互为相反数,将y=x和y=-x分别代入(1)中所求的解析式,得到关于x的一元二次方程,解方程求出x的值,再得到y的值,即可求解.
解答:解:(1)∵抛物线y=ax2+bx+c经过P(0,-1)、Q(1,2)、M(-3,2)三点,
∴
,解得
,
∴此抛物线的表达式为y=x2+2x-1;
(2)①将y=x代入y=x2+2x-1,得x2+2x-1=x,
整理得,x2+x-1=0,
解得x=
,
所以此抛物线上到两坐标轴距离相等的点的坐标为(
,
),(
,
);
②将y=-x代入y=x2+2x-1,得x2+2x-1=-x,
整理得,x2+3x-1=0,
解得x=
,
所以此抛物线上到两坐标轴距离相等的点的坐标为(
,
),(
,
);
综上所述,此抛物线上到两坐标轴距离相等的点的坐标为(
,
),(
,
),(
,
),(
,
).
∴
|
|
∴此抛物线的表达式为y=x2+2x-1;
(2)①将y=x代入y=x2+2x-1,得x2+2x-1=x,
整理得,x2+x-1=0,
解得x=
-1±
| ||
| 2 |
所以此抛物线上到两坐标轴距离相等的点的坐标为(
-1+
| ||
| 2 |
-1+
| ||
| 2 |
-1-
| ||
| 2 |
-1-
| ||
| 2 |
②将y=-x代入y=x2+2x-1,得x2+2x-1=-x,
整理得,x2+3x-1=0,
解得x=
-3±
| ||
| 2 |
所以此抛物线上到两坐标轴距离相等的点的坐标为(
-3+
| ||
| 2 |
3-
| ||
| 2 |
-3-
| ||
| 2 |
3+
| ||
| 2 |
综上所述,此抛物线上到两坐标轴距离相等的点的坐标为(
-1+
| ||
| 2 |
-1+
| ||
| 2 |
-1-
| ||
| 2 |
-1-
| ||
| 2 |
-3+
| ||
| 2 |
3-
| ||
| 2 |
-3-
| ||
| 2 |
3+
| ||
| 2 |
点评:本题考查了用待定系数法求二次函数的解析式.在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
下列说法中正确的是( )
| A、延长射线OA到点B |
| B、线段AB为直线AB的一部分 |
| C、射线OM与射线MO表示同一条射线 |
| D、一条直线由两条射线组成 |
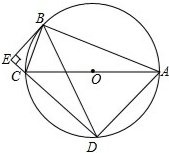 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,BC=5,BE⊥DC交DC的延长线于点E.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,BC=5,BE⊥DC交DC的延长线于点E. 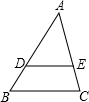 如图,在△ABC中,在D,E分别在AB、AC上,且DE∥BC.若
如图,在△ABC中,在D,E分别在AB、AC上,且DE∥BC.若