题目内容
通分:
与
.
| 2 |
| 3(3-a) |
| a-1 |
| (a-3)(a+3) |
考点:通分
专题:计算题
分析:先确定最简公分母为3(a-3)(a+3),然后利用分式的基本性质把两个分式的分母化为3(a-3)(a+3)即可.
解答:解:最简公分母为3(a-3)(a+3),
=-
;
=
.
| 2 |
| 3(3-a) |
| 2(a+3) |
| 3(a-3)(a+3) |
| a-1 |
| (a-3)(a+3) |
| 3(a-1) |
| 3(a-3)(a+3) |
点评:本题考查了通分:把几个异分母的分式分别化为与原来的分式相等的同分母的分式,这样的分式变形叫做分式的通分.通分的关键是确定最简公分母.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
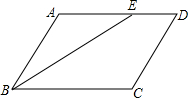 如图,在四边形ABCD中,已知BE平分∠ABC,交AD于E,∠AEB=∠ABE.
如图,在四边形ABCD中,已知BE平分∠ABC,交AD于E,∠AEB=∠ABE.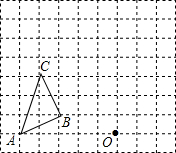 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2: 已知:如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.
已知:如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.