题目内容
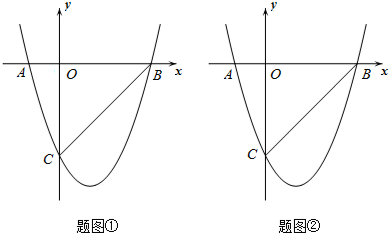
在平面直角坐标系中,点O为坐标原点,抛物线y=x2+
cx+c与x轴的负半轴交于点A,与x轴的正半轴交于点B,与y轴交于点C,直线BC的解析式为:y=x+c.
(1)求抛物线的解析式;
(2)点P在抛物线y=x2+
cx+c位于第四象限的部分上,连接PC,若PC⊥BC,求点P的坐标;
(3)在(2)的条件下,过点C作y轴的垂线,交抛物线y=x2+
cx+c于另一点E,动点Q在抛物线y=x2+
cx+c上,且点Q在B、E两点之间(点Q不与B、E重合),过点Q作QH⊥x轴于点H,直线QH与直线CE交于点R,连接PQ、PR,PQ交CR于点N,求证:PR2=PN•PQ.
| 2 |
| 3 |
(1)求抛物线的解析式;
(2)点P在抛物线y=x2+
| 2 |
| 3 |
(3)在(2)的条件下,过点C作y轴的垂线,交抛物线y=x2+
| 2 |
| 3 |
| 2 |
| 3 |

考点:二次函数综合题
专题:
分析:(1)首先表示出点C的坐标,然后代入二次函数的解析式利用待定系数法确定二次函数的解析式即可;
(2)过点P做PD⊥y轴于点D,根据B(3,0),C(0,-3)的坐标得到△OBC和△PCD均为等腰直角三角形,设PD=CD=a,根据点P在抛物线y=x2-2x-3上得到OD=点P的纵坐标的绝对值=-(a2-2a-3),从而得到3+a=-(a2-2a-3),求得a的值后即可求得点P的坐标;
(3)过点P作PK⊥QH交HQ的延长线于点K,设点Q的横坐标为m,则点Q的纵坐标为m2-2m-3,从而表示出QH=-(m2-2m-3)、PK=m-1,QK=KH-QH=4+m2-2m-3=m2-2m+1,然后利用tan∠PRK=tan∠PQK得到∠PRK=∠PQK,从而得到
=
,证得△KPR∽△KQP,得到∠KPR=∠KQP,从而证得△PRN∽△PQR,然后利用相似三角形对应边成比例列出比例式,从而得到等积式.
(2)过点P做PD⊥y轴于点D,根据B(3,0),C(0,-3)的坐标得到△OBC和△PCD均为等腰直角三角形,设PD=CD=a,根据点P在抛物线y=x2-2x-3上得到OD=点P的纵坐标的绝对值=-(a2-2a-3),从而得到3+a=-(a2-2a-3),求得a的值后即可求得点P的坐标;
(3)过点P作PK⊥QH交HQ的延长线于点K,设点Q的横坐标为m,则点Q的纵坐标为m2-2m-3,从而表示出QH=-(m2-2m-3)、PK=m-1,QK=KH-QH=4+m2-2m-3=m2-2m+1,然后利用tan∠PRK=tan∠PQK得到∠PRK=∠PQK,从而得到
| KP |
| KQ |
| KR |
| KP |
解答:解:(1)∵对于y=x+c,当y=0时,x=-c,
∴B(-c,0),
代入y=x2+
cx+c,解答:c=0,或c=-3,
∴
c=
×(-3)=-2,
∴抛物线的解析式为y=x2-2x-3;
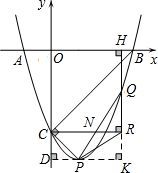 (2)如图,过点P做PD⊥y轴于点D,
(2)如图,过点P做PD⊥y轴于点D,
由(1)知B(3,0),C(0,-3),
∴OB=OC=3,
∴△OBC为等腰直角三角形,
∵PC⊥BC,
∴∠PCD=∠CBO=45°
∴△PCD为等腰直角三角形,
设PD=CD=a,
∵点P在抛物线y=x2-2x-3上,
∴OD=点P的纵坐标的绝对值=-(a2-2a-3),
∴3+a=-(a2-2a-3),
解得:a=0(舍去)或a=1,
把a=1代入y=x2-2x-3中得y=4,
∴点P的坐标为(1,-4);
(3)过点P作PK⊥QH交HQ的延长线于点K,如图,
设点Q的横坐标为m,则点Q的纵坐标为m2-2m-3,
∴QH=-(m2-2m-3),
∵P(1,4),
∴KH=4,
∴PK=m-1,QK=KH-QH=4+m2-2m-3=m2-2m+1,
∵四边形CDKR为矩形,
∴RK=CD=1,
在Rt△PRK和Rt△PQK中,∠K=90°,
tan∠PRK=
=
,
tan∠PQK=
=
=
,
即tan∠PRK=tan∠PQK,
∴∠PRK=∠PQK,
∵KR=CD=4-3=1,
∴
=
,
即
=
,
∵∠K=∠K,
∴△KPR∽△KQP,
∴∠KPR=∠KQP,
∵PK∥CR,
∴∠RPK=∠PRN,
∠PRN=∠PQR,
而∠RPN=∠QPR,
∴△PRN∽PQR,
∴
=
,
∴PR2=PN•PQ.
∴B(-c,0),
代入y=x2+
| 2 |
| 3 |
∴
| 2 |
| 3 |
| 2 |
| 3 |
∴抛物线的解析式为y=x2-2x-3;
 (2)如图,过点P做PD⊥y轴于点D,
(2)如图,过点P做PD⊥y轴于点D,由(1)知B(3,0),C(0,-3),
∴OB=OC=3,
∴△OBC为等腰直角三角形,
∵PC⊥BC,
∴∠PCD=∠CBO=45°
∴△PCD为等腰直角三角形,
设PD=CD=a,
∵点P在抛物线y=x2-2x-3上,
∴OD=点P的纵坐标的绝对值=-(a2-2a-3),
∴3+a=-(a2-2a-3),
解得:a=0(舍去)或a=1,
把a=1代入y=x2-2x-3中得y=4,
∴点P的坐标为(1,-4);
(3)过点P作PK⊥QH交HQ的延长线于点K,如图,
设点Q的横坐标为m,则点Q的纵坐标为m2-2m-3,
∴QH=-(m2-2m-3),
∵P(1,4),
∴KH=4,
∴PK=m-1,QK=KH-QH=4+m2-2m-3=m2-2m+1,
∵四边形CDKR为矩形,
∴RK=CD=1,
在Rt△PRK和Rt△PQK中,∠K=90°,
tan∠PRK=
| RK |
| PK |
| 1 |
| m-1 |
tan∠PQK=
| PK |
| QK |
| m-1 |
| m2-2m+1 |
| 1 |
| m-1 |
即tan∠PRK=tan∠PQK,
∴∠PRK=∠PQK,
∵KR=CD=4-3=1,
∴
| m-1 |
| (m-1)2 |
| 1 |
| m-1 |
即
| KP |
| KQ |
| KR |
| KP |
∵∠K=∠K,
∴△KPR∽△KQP,
∴∠KPR=∠KQP,
∵PK∥CR,
∴∠RPK=∠PRN,
∠PRN=∠PQR,
而∠RPN=∠QPR,
∴△PRN∽PQR,
∴
| PR |
| PQ |
| PN |
| PR |
∴PR2=PN•PQ.
点评:本题考查了二次函数的综合知识,还涉及到了待定系数法确定二次函数的解析式、相似三角形的判定与性质等知识,综合性较强,难度较大.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
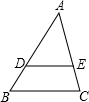 如图,在△ABC中,在D,E分别在AB、AC上,且DE∥BC.若
如图,在△ABC中,在D,E分别在AB、AC上,且DE∥BC.若