题目内容
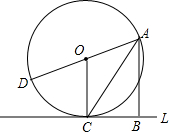如图所示，直线L切⊙O于点C，AD为⊙O的任意一条直径，点B在直线L上，且∠BAC=∠CAD（AD与AB不在一条直线上），试判断四边形ABCO为怎样的特殊四边形？考点：切线的性质
专题：常规题型
分析：先根据切线的性质得到OC⊥BC，再证明OC∥AB，然后分类讨论：当AD不平行L时，可判断四边形ABCO为直角梯形；当AD平行L时，可判断四边形ABCO为矩形．
解答：解：四边形ABCO为直角梯形或矩形．理由如下：
∵直线L切⊙O于点C，
∴OC⊥BC，
∵OA=OC，
∴∠OAC=∠OCA，
而∠BAC=∠CAD，
∴∠BAC=∠OCA，
∴OC∥AB，
当AD不平行L时，四边形ABCO为直角梯形；
当AD平行L时，四边形ABCO为矩形．
∵直线L切⊙O于点C，
∴OC⊥BC，
∵OA=OC，
∴∠OAC=∠OCA，
而∠BAC=∠CAD，
∴∠BAC=∠OCA，
∴OC∥AB，
当AD不平行L时，四边形ABCO为直角梯形；
当AD平行L时，四边形ABCO为矩形．
点评：本题考查了圆的切线的性质：圆的切线垂直于经过切点的半径．也考查了直角梯形和矩形的判定方法．
练习册系列答案
相关题目
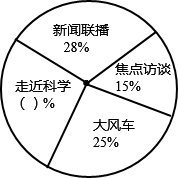如图是某学校教师喜欢看的电视节目统计图．
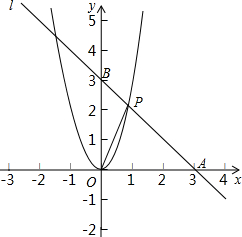如图，直线l过A（3，0）和B（0，3）两点，它与二次函数y=ax2的图象在第一象限内交于点P，若△AOP的面积为3，求二次函数的表达式．
如图，在△ABC中，∠B=90°，∠C=30°，AB=3，BC=3
如图所示，等边三角形的高为a，P为BC边上（与BC不重合）的任意一点，且PD⊥AB于点D，PE⊥AC于E，则PE+PD=
如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，BC=5，BE⊥DC交DC的延长线于点E．