题目内容
10．
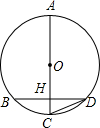如图，AC为⊙O直径，AC=10，弦BD⊥AC于H，∠BDC=30°，则BH为（ ）| A． | $\frac{5}{2}$ | B． | $\frac{{5\sqrt{5}}}{2}$ | C． | $\frac{{5\sqrt{3}}}{2}$ | D． | 4 |
分析 连接OB，根据圆周角定理求出∠BOC，求出OB，解直角三角形求出BH即可．
解答 解：连接OB，
∵∠BDC=30°，
∴∠BOC=2∠BDC=60°，
∵AC为⊙O直径，AC=10，
∴OB=5，
∵BD⊥AC，
∴∠BHO=90°，
∴BH=OB×sin60°=5×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{2}$．
故选C．
点评 本题考查了垂径定理，解直角三角形，圆周角定理的应用，能求出∠BOC的度数是解此题的关键．
练习册系列答案
通城学典默写能手系列答案
相关题目
20．
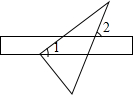将一块含60°角的直角三角板和直尺如图放置，使三角板的直角顶点落在直尺的一边上，若∠1=40°，则∠2的度数是（ ）
将一块含60°角的直角三角板和直尺如图放置，使三角板的直角顶点落在直尺的一边上，若∠1=40°，则∠2的度数是（ ）| A． | 90° | B． | 80° | C． | 75° | D． | 70° |
18．某水库养殖场连续用20天时间，采用每天降低水位以减少捕捞成本的办法，对水库中某种鲜鱼进行捕捞、销售．根据调查，整理出第x天（1≤x≤20且x为整数）的捕捞与销售的相关信息如表：
（1）假定该养殖场每天捕捞和销售的鲜鱼没有损失，且能在当天全部售出，求第x天的收入y（元）与x（元）之间的函数关系式；（当天收入=日销售额-日捕捞成本）
（2）试说明（1）中的函数y随x的变化情况，并指出在第几天y取得最大值，最大值是多少？
| 鲜鱼销售单价（元/kg） | 20 |
| 单位捕捞成本（元/kg） | $5-\frac{x}{5}$ |
| 捕捞量（kg） | 950-10x |
（2）试说明（1）中的函数y随x的变化情况，并指出在第几天y取得最大值，最大值是多少？
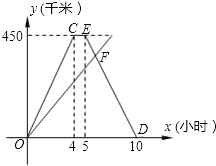A、B两城间的公路长为450千米，甲、乙两车同时从A城出发沿这一公路驶向B城，甲车到达B城1小时后沿原路返回．如图是它们离A城的路程y（千米）与行驶时间 x（小时）之间的函数图象．