题目内容
20．已知A÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+4xy+4{y}^{2}}$=$\frac{x+2y}{x+y}$，当x=2，y=1时，求A的值．分析 根据被除数=除数×商，求出A，将x与y的值代入计算即可求出值．
解答 解：由A÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+4xy+4{y}^{2}}$=$\frac{x+2y}{x+y}$，得到A=$\frac{x+2y}{x+y}$•$\frac{（x+y）（x-y）}{（x+2y）^{2}}$=$\frac{x-y}{x+2y}$，
当x=2，y=1时，原式=$\frac{1}{4}$．
点评 此题考查了分式的乘除法，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
10．
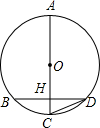如图，AC为⊙O直径，AC=10，弦BD⊥AC于H，∠BDC=30°，则BH为（ ）
如图，AC为⊙O直径，AC=10，弦BD⊥AC于H，∠BDC=30°，则BH为（ ）| A． | $\frac{5}{2}$ | B． | $\frac{{5\sqrt{5}}}{2}$ | C． | $\frac{{5\sqrt{3}}}{2}$ | D． | 4 |
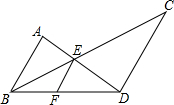如图，F在BD上，BC，AD相交于点E，且AB∥CD∥EF．