题目内容
5．有三个形状和材质一样的盒子里分别装有3个红球、6个黄球、9个黑球，蒙着眼睛随机从盒子中摸出一个球是黑球的概率为$\frac{1}{2}$．分析 根据概率的求法，找准两点：
①全部情况的总数为18；
②符合条件的情况数目为9；二者的比值就是其发生的概率．
解答 解：∵黑球共有9个，球数共有6+3+9=18个，
∴P（黑球）=$\frac{9}{18}$=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 本题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．
练习册系列答案
相关题目
如图，直线l1∥l2，AC=10，DE=3，EF=2，则AB的长是6．
16．下列函数，一定是二次函数的是（ ）
| A． | y=x2-$\frac{1}{x}$ | B． | y=ax2+bx+c | C． | y=（x-3）2-x2 | D． | y=（m2+1）x2（m为常数） |
如图，⊙O中弦AB，CD相交于点P，已知AP=3，BP=2，CP=1，则DP=6．
10．
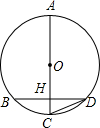如图，AC为⊙O直径，AC=10，弦BD⊥AC于H，∠BDC=30°，则BH为（ ）
如图，AC为⊙O直径，AC=10，弦BD⊥AC于H，∠BDC=30°，则BH为（ ）| A． | $\frac{5}{2}$ | B． | $\frac{{5\sqrt{5}}}{2}$ | C． | $\frac{{5\sqrt{3}}}{2}$ | D． | 4 |
14．若点A（a+1，b-1）在第二象限，则点B（-a，b+2）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |