Question

12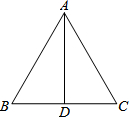．如图，在△ABC中，已知AB=AC，AD⊥BC于点D．请写出图中的等量关系，并说明等量关系成立的理由．

Answer 1

分析 根据等腰三角形的性质和垂直得出∠B=∠C，BD=DC，AD平分∠BAC，∠ADC=∠ADB=90°，证△ADB≌△ADC，即可的面积相等，周长相等．

解答 解：∵AB=AC，AD⊥BC，
∴∠B=∠C（等边对等角），BD=DC，AD平分∠BAC（三线合一定理），∠ADC=∠ADB=90°（垂直定义），
在△ADB和△ADC中
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$
∴△ADB≌△ADC，
∴S_△ADB=S_△ADC=$\frac{1}{2}$S_△ABC，△ADB的周长=△ADC的周长．

点评 本题考查了等腰三角形的性质，全等三角形的性质和判定的应用，能熟记等腰三角形的性质是解此题的关键，注意：①等边对等角，②等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合（三线合一定理）．