题目内容
17.如图1,Rt△ABC中,∠ACB=90°,D为AB的中点,∠EDF=90°,DE交AC于点G,DF经过点C.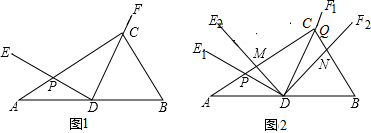
(1)若∠B=60°.
①求∠ADE的度数;
②如图2,将图1中的∠EDF绕点D顺时针方向旋转角α(0°<α<60°),旋转过程中的任意两个位置分别记为∠E1DF1,∠E2DF2,DE1交直线AC于点P,DF1交直线BC于点Q,DE2交直线AC于点M,DF2交直线BC于点N,求$\frac{PM}{QN}$的值;
(2)将(1)问中的“若∠B=60°”改为“∠B=β(60°<β<90°)”,其余条件不变,判断$\frac{PM}{QN}$的值是否为定值,如果是,请直接写出这个值(用含β的式子表示);如果不是,请说明理由.
分析 (1)根据含30°的直角三角形的性质和等边三角形的性质解答即可;
(2)根据相似三角形的判定和性质以及直角三角形中的三角函数解答即可;
(3)由(2)的推理得出 $\frac{PM}{QN}$,再利用直角三角形的三角函数解答.
解答 解:(1)①∵∠ACB=90°,D为AB的中点,
∴CD=DB,
∴∠DCB=∠B,
∵∠B=60°,
∴∠DCB=∠B=∠CDB=60°,
∴∠CDA=120°,
∵∠EDC=90°,
∴∠ADE=30°;
②∵∠C=90°,∠MDN=90°,
∴∠DMC+∠CND=180°,
∵∠DMC+∠PMD=180°,
∴∠CND=∠PMD,
同理∠CPD=∠DQN,
∴△PMD∽△QND,
过点D分别做DG⊥AC于G,DH⊥BC于H,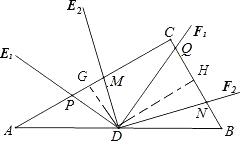
可知DG,DH分别为△PMD和△QND的高
∴$\frac{PM}{QN}$=$\frac{DG}{DH}$,
∵DG⊥AC于G,DH⊥BC于H,
∴DG∥BC,
又∵D为AC中点,
∴G为AC中点,
∵∠C=90°,
∴四边形CGDH 为矩形有CG=DH=AG,
Rt△AGD中,$\frac{DG}{AG}$=$\frac{1}{\sqrt{3}}$,
即 $\frac{PM}{QN}$=$\frac{\sqrt{3}}{3}$
(2)是定值,定值为tan(90°-β),
∵$\frac{PM}{QN}$=$\frac{DG}{DH}$,四边形CGDH 为矩形有CG=DH=AG,
∴Rt△AGD中,$\frac{DG}{AG}$=tan∠A=tan(90°-∠B)=tan(90°-β),
∴$\frac{PM}{QN}$=tan(90°-β).
点评 此题是几何变换综合题,组要考查了矩形的性质,锐角三角函数的定义相似三角形的性质和判定,关键是根据直角三角形的性质和相似三角形的判定进行解答

①a∥b;②b∥c;③a∥c;④a⊥b;⑤a⊥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是( )
| A. | 已知①②则③ | B. | 已知②⑤则④ | C. | 已知②④则③ | D. | 已知④⑤则② |
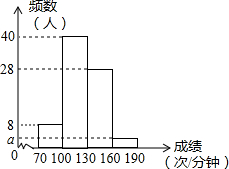 阳光体育运动关乎每个学生未来的幸福生活,今年四月份,我区某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班级2-3名选手参赛,现将80名选手比赛成绩(次/min)进行统计.绘制如图所示的频数分布直方图,则图中a的值为4.
阳光体育运动关乎每个学生未来的幸福生活,今年四月份,我区某校开展了以“阳光体育我是冠军”为主题的一分钟限时跳绳比赛,要求每个班级2-3名选手参赛,现将80名选手比赛成绩(次/min)进行统计.绘制如图所示的频数分布直方图,则图中a的值为4.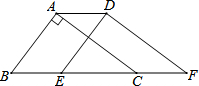 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论①AC∥DF;②ED⊥DF;③四边形ABFD的周长是16.其中正确的个数为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论①AC∥DF;②ED⊥DF;③四边形ABFD的周长是16.其中正确的个数为( )