题目内容
15.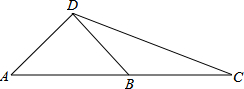 如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.
如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.
分析 延长DB至E,使BE=BD,连接CE,然后利用“边角边”证明△ABD和△CBE全等,根据全等三角形对应角相等可得∠ADB=∠E,∠DBA=∠EBC,设CE=x,利用直角三角形30°角所对的直角边等于斜边的一半可得CD=2x,利用勾股定理列式求出DE,再求出BE,然后利用勾股定理列式求出BC,再利用锐角三角函数的余弦等于邻边比斜边列式计算即可得解.
解答 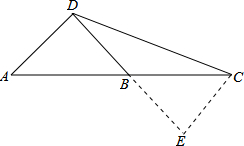 解:如图,延长DB至E,使BE=BD,连接CE,
解:如图,延长DB至E,使BE=BD,连接CE,
∵B是AC的中点,
∴AB=BC.
在△ABD和△CBE中,
$\left\{\begin{array}{l}{AB=CB}\\{∠ABD=∠CBE}\\{BD=BE}\end{array}\right.$,
∴△ABD≌△CBE(SAS),
∴∠ADB=∠E,∠DBA=∠EBC,
∵AD⊥BD,
∴∠ADB=90°,
∴∠E=90°.
设CE=x,∵∠BDC=30°,
∴CD=2CE=2x,
由勾股定理得DE=$\sqrt{(2x)^{2}-{x}^{2}}$=$\sqrt{3}$x,
∴BE=$\frac{\sqrt{3}}{2}$x,
在Rt△BCE中,BC=$\sqrt{B{E}^{2}+C{E}^{2}}$=$\sqrt{(\frac{\sqrt{3}}{2}x)^{2}+{x}^{2}}$=$\frac{\sqrt{7}}{2}$x,
∴cos∠DBA=cos∠EBC=$\frac{BE}{BC}$=$\frac{\frac{\sqrt{3}}{2}x}{\frac{\sqrt{7}}{2}x}$=$\frac{\sqrt{21}}{7}$.
点评 本题考查了全等三角形的判定与性质,勾股定理,锐角三角函数的定义,直角三角形30°角所对的直角边等于斜边的一半的性质,难点在于作辅助线构造出全等三角形.

| A. | d=r | B. | d<r | C. | d>r | D. | d≤r |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
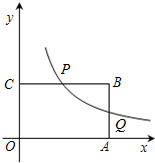 反比例函数y=$\frac{1}{x}$经过矩形COAB中CB的中点P,交AB于点Q,已知点P的横坐标为a.
反比例函数y=$\frac{1}{x}$经过矩形COAB中CB的中点P,交AB于点Q,已知点P的横坐标为a. 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P,Q同时从A,B两点出发,分别沿AC,BC向终点C移动,它们的速度都是1cm/s,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后可使△PCQ的面积为Rt△ABC面积的一半?
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P,Q同时从A,B两点出发,分别沿AC,BC向终点C移动,它们的速度都是1cm/s,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后可使△PCQ的面积为Rt△ABC面积的一半?
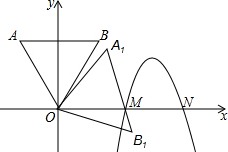 如图,抛物线y=a(x-$\sqrt{6}$-1)2+3与x轴交于M,N两点,正三角形OAB边长为$\sqrt{3}$+1,且AB垂直y轴,将正三角形OAB绕顶点O顺时针旋转75°得正三角形OA1B1,边A1B1恰好经过点M,则a的值为-3.
如图,抛物线y=a(x-$\sqrt{6}$-1)2+3与x轴交于M,N两点,正三角形OAB边长为$\sqrt{3}$+1,且AB垂直y轴,将正三角形OAB绕顶点O顺时针旋转75°得正三角形OA1B1,边A1B1恰好经过点M,则a的值为-3. 如图,AD是△ABC的角平分线,AB=AC,点E、F分别是AB、AC的中点.
如图,AD是△ABC的角平分线,AB=AC,点E、F分别是AB、AC的中点.