题目内容
3. 如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P,Q同时从A,B两点出发,分别沿AC,BC向终点C移动,它们的速度都是1cm/s,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后可使△PCQ的面积为Rt△ABC面积的一半?
如图,在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.点P,Q同时从A,B两点出发,分别沿AC,BC向终点C移动,它们的速度都是1cm/s,且当其中一点到达终点时,另一点也随之停止移动.问点P,Q出发几秒后可使△PCQ的面积为Rt△ABC面积的一半?
分析 设点P,Q出发x秒后可使△PCQ的面积为Rt△ABC面积的一半,AP=xcm,PC=(6-x)cm,CQ=(8-x)cm,此时△PCQ的面积为:$\frac{1}{2}$×(8-x)(6-x),令该式=12,由此等量关系列出方程求出符合题意的值.
解答 解:设点P,Q出发x秒后可使△PCQ的面积为Rt△ABC面积的一半,由题意得:
S△ABC=$\frac{1}{2}$×AC•BC=$\frac{1}{2}$×6×8=24,
即:$\frac{1}{2}$×(8-x)×(6-x)=$\frac{1}{2}$×24,
x2-14x+24=0,
(x-2)(x-12)=0,
x1=12(舍去),x2=2.
答:点P,Q出发2秒后可使△PCQ的面积为Rt△ABC面积的一半.
点评 此题主要考查了一元二次方程的应用,关键在于表示出三角形面积进而得出等量关系求解.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
13.(a+$\frac{1}{2}$b)2等于( )
| A. | a2+$\frac{1}{4}$b2 | B. | a2+2ab+$\frac{1}{4}$b2 | C. | a2+$\frac{1}{4}$ab+$\frac{1}{4}$b2 | D. | a2+ab+$\frac{1}{4}$b2 |
11. 如图,已知校门的坐标是(1,1),那么下列对于实验楼位置的叙述正确的个数为( )
如图,已知校门的坐标是(1,1),那么下列对于实验楼位置的叙述正确的个数为( )
①实验楼的坐标是3;②实验楼的坐标是(3,3);③实验楼的坐标为(4,4);④实验楼在校门的东北方向上,距校门大约283米.
 如图,已知校门的坐标是(1,1),那么下列对于实验楼位置的叙述正确的个数为( )
如图,已知校门的坐标是(1,1),那么下列对于实验楼位置的叙述正确的个数为( )①实验楼的坐标是3;②实验楼的坐标是(3,3);③实验楼的坐标为(4,4);④实验楼在校门的东北方向上,距校门大约283米.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.在方格纸上有A、B两点,若以B点为原点建立直角坐标系,则A点坐标为(2,5),若以A点为原点建立直角坐标系,则B点坐标为( )
| A. | (-2,-5) | B. | (-2,5) | C. | (2,-5) | D. | (2,5) |
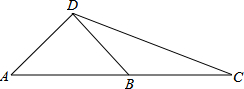 如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.
如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.