题目内容
5.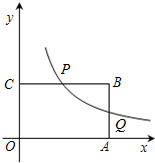 反比例函数y=$\frac{1}{x}$经过矩形COAB中CB的中点P,交AB于点Q,已知点P的横坐标为a.
反比例函数y=$\frac{1}{x}$经过矩形COAB中CB的中点P,交AB于点Q,已知点P的横坐标为a.(1)求点Q的坐标.(用含a的字母表示)
(2)试说明点Q是AB的中点.
分析 (1)直接把点P的横坐标代入反比例函数y=$\frac{1}{x}$即可得出其纵坐标,再由点P是点Q的中点得出点Q的坐标;
(2)求出B点的坐标与Q点的坐标相比较即可得出结论.
解答 解:(1)∵点P是BC的中点,且点P在反比例函数y=$\frac{1}{x}$上,
∴P(a,$\frac{1}{a}$).
∵点Q在直线AB上,
∴点Q的横坐标为2a,
∴Q(2a,$\frac{1}{2a}$);
(2)∵P(a,$\frac{1}{a}$),点P是BC的中点,
∴B(2a,$\frac{1}{a}$).
∵Q(2a,$\frac{1}{2a}$),
∴点Q是AB的中点.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
13.(a+$\frac{1}{2}$b)2等于( )
| A. | a2+$\frac{1}{4}$b2 | B. | a2+2ab+$\frac{1}{4}$b2 | C. | a2+$\frac{1}{4}$ab+$\frac{1}{4}$b2 | D. | a2+ab+$\frac{1}{4}$b2 |
20.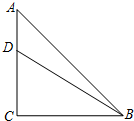 如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
 如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )| A. | 4 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
10.王英同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地( )
| A. | 50m | B. | 100$\sqrt{3}$m | C. | 150m | D. | 100m |
17. 如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
 如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )| A. | 100m | B. | 100$\sqrt{3}$m | C. | 50$\sqrt{3}$m | D. | $50({\sqrt{3}+1})$m |
 表示运算a-b+c,图形
表示运算a-b+c,图形 表示运算x+z-y-w.则
表示运算x+z-y-w.则 +
+ =0
=0 如图,已知一次函数y1=k1x+2的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A,B 两点,且A(-4,m)、B(8,-2).
如图,已知一次函数y1=k1x+2的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A,B 两点,且A(-4,m)、B(8,-2).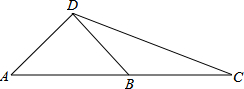 如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.
如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.