题目内容
20.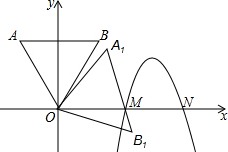 如图,抛物线y=a(x-$\sqrt{6}$-1)2+3与x轴交于M,N两点,正三角形OAB边长为$\sqrt{3}$+1,且AB垂直y轴,将正三角形OAB绕顶点O顺时针旋转75°得正三角形OA1B1,边A1B1恰好经过点M,则a的值为-3.
如图,抛物线y=a(x-$\sqrt{6}$-1)2+3与x轴交于M,N两点,正三角形OAB边长为$\sqrt{3}$+1,且AB垂直y轴,将正三角形OAB绕顶点O顺时针旋转75°得正三角形OA1B1,边A1B1恰好经过点M,则a的值为-3.
分析 根据题意求得∠A1OM=45°,作A1C⊥OM于C,解等腰直角三角形求得A1C=OC=$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1),作∠A1MD=15°,交A1C于D,得出∠MDC=30°,A1D=DM,解直角三角形求得CM=$\frac{\sqrt{2}}{2}$($\sqrt{3}$-1),即可求得M的坐标,代入抛物线的解析式,利用待定系数法即可求得.
解答  解:∵∠BOB1=75°,∠A1OB1=60°,
解:∵∠BOB1=75°,∠A1OB1=60°,
∴∠A′OB=15°,
∵AB垂直y轴,
∴∠1=30°,
∴∠A1OM=45°,
作A1C⊥OM于C,
∴∠OA1C=45°,
∴∠MA1C=15°,
∵OA1=$\sqrt{3}$+1,
∴A1C=OC=$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1),
作∠A1MD=15°,交A1C于D,
∴∠MDC=30°,A1D=DM,
∴DM=2CM,设CM=x,则A1D=DM=2x,
∴DC=$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1)-2x,
∵tan∠MDC=$\frac{MC}{DC}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{x}{\frac{\sqrt{2}}{2}(\sqrt{3}+1)-2x}$=$\frac{\sqrt{3}}{3}$
∴(3+2$\sqrt{3}$)x=$\frac{\sqrt{2}}{2}$(3+$\sqrt{3}$),
解得x=$\frac{\sqrt{2}}{2}$($\sqrt{3}$-1),
∴CM=$\frac{\sqrt{2}}{2}$($\sqrt{3}$-1),
∴OM=OC+CM=$\frac{\sqrt{2}}{2}$($\sqrt{3}$+1)+$\frac{\sqrt{2}}{2}$($\sqrt{3}$-1)=$\sqrt{6}$,
∴M($\sqrt{6}$,0),
代入y=a(x-$\sqrt{6}$-1)2+3得,0=a($\sqrt{6}$-$\sqrt{6}$-1)2+3,
解得a=-3.
故答案为-3.
点评 本题考查了等腰直角三角形的判定和性质,解直角三角函数,待定系数法求解析式等,作出辅助线构建直角三角形是解题的关键.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案| A. | 50m | B. | 100$\sqrt{3}$m | C. | 150m | D. | 100m |
 如图,已知校门的坐标是(1,1),那么下列对于实验楼位置的叙述正确的个数为( )
如图,已知校门的坐标是(1,1),那么下列对于实验楼位置的叙述正确的个数为( )①实验楼的坐标是3;②实验楼的坐标是(3,3);③实验楼的坐标为(4,4);④实验楼在校门的东北方向上,距校门大约283米.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | (-2,-5) | B. | (-2,5) | C. | (2,-5) | D. | (2,5) |
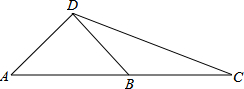 如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.
如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦. 如图,在△ABC中,D是AB的中点,F是BC边延长线上的点,连结DF交AC于点E.求证:CF:BF=CE:AE.(提示:过点C作CG∥AB)
如图,在△ABC中,D是AB的中点,F是BC边延长线上的点,连结DF交AC于点E.求证:CF:BF=CE:AE.(提示:过点C作CG∥AB)