题目内容
7. 如图,AD是△ABC的角平分线,AB=AC,点E、F分别是AB、AC的中点.
如图,AD是△ABC的角平分线,AB=AC,点E、F分别是AB、AC的中点.求证:四边形AEDF是菱形.
分析 首先根据AD是△ABC的角平分线,AB=AC,利用等腰三角形的性质得出点D是BC的中点,进一步利用三角形的中位线定理证得结论成立即可.
解答 证明:∵AD是△ABC的角平分线,AB=AC,
∴点D是BC的中点,
∵点E、F分别是AB、AC的中点,
∴DE,EF是三角形的中位线,
∴DE∥AB,DF∥AC,
∴四边形ADEF是平行四边形,
∵AB=AC,
点E,F分别是AB,AC的中点,
∴AE=AF,
∴平行四边形ADEF为菱形.
点评 本题考查了菱形的判定.利用了三角形的中位线的性质和平行四边形的判定和性质、等腰三角形的性质解决问题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
17. 如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
 如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )
如图所示,从山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100m,点C在BD上,则山高AB为( )| A. | 100m | B. | 100$\sqrt{3}$m | C. | 50$\sqrt{3}$m | D. | $50({\sqrt{3}+1})$m |
2.若x+y=9,x-y=1,则代数式2134-3(x2+y2)的值是( )
| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
19.在实数0,$\frac{1}{3}$,$\sqrt{3}$,2.57,$\frac{π}{2}$中无理数的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
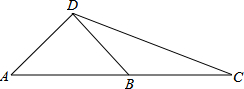 如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.
如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.