题目内容
10.已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A 作AG⊥BE于G,AG、BD交于F,求证:OE=OF
②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB延长线于点F,其它条件不变,OE=OF还成立吗?

分析 ①由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可;
②由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可.
解答 ①证明:∵四边形ABCD是正方形,
∴OA=OB,AC⊥BD,
∴∠BOE=∠AOF=90°,
∴∠OEB+∠OBE=90°,
∵AG⊥BE,
∴∠AGE=90°,
∴∠OEB+∠OAF=90°,
∴∠OBE=∠OAF,
在△BOE和△AOF中,
$\left\{\begin{array}{l}{∠BOE=∠AOF}&{\;}\\{OB=OA}&{\;}\\{∠OBE=∠OAF}&{\;}\end{array}\right.$,
∴△BOE≌△AOF(ASA),
∴OE=OF;
②解:OE=OF还成立;理由如下:
∵四边形ABCD是正方形,
∴OA=OB,AC⊥BD,
∴∠BOE=∠AOF=90°,
∴∠OEB+∠OBE=90°,
∵AG⊥BE,
∴∠AGE=90°,
∴∠OEB+∠OAF=90°,
∴∠OBE=∠OAF,
在△BOE和△AOF中,
$\left\{\begin{array}{l}{∠BOE=∠AOF}&{\;}\\{OB=OA}&{\;}\\{∠OBE=∠OAF}&{\;}\end{array}\right.$,
∴△BOE≌△AOF(ASA),
∴OE=OF.
点评 本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
20.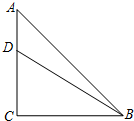 如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
 如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )
如图,在等腰Rt△ABC中,∠C=90°,AC=12,D是AC上一点,若tan∠DBA=$\frac{1}{5}$,则AD的长为( )| A. | 4 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
2.若x+y=9,x-y=1,则代数式2134-3(x2+y2)的值是( )
| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
19.在实数0,$\frac{1}{3}$,$\sqrt{3}$,2.57,$\frac{π}{2}$中无理数的个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
20.水库管理人员为掌握水库蓄水情况,需要观测水库水位变化,下表是一周内水位高低的变化情况,用正数表示水位比前一天上升数,用负数表示水位比前一天下降数.
(1)问水库的水位在本周内是上升还是下降,幅度是多少米?
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 水位变化(米) | 0.12 | -0.02 | -0.13 | -0.20 | -0.08 | -0.02 | 0.32 |
(2)这一周内,哪一天水库的水位最高?哪一天的水位最低?最高水位比最低水位高多少?
 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,使点C与点A重合,点D落在点G处,求线段BF的长.
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,使点C与点A重合,点D落在点G处,求线段BF的长.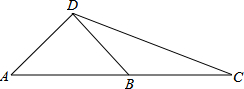 如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.
如图,AD⊥BD,∠CDB=30°,B为AC的中点,求∠DBA的余弦.