题目内容
已知a、b是方程x2+x-2015=0的两个实数根,求:a2+2a+b的值.
考点:根与系数的关系
专题:
分析:先根据一元二次方程的解的定义得到a2+a-2015=0,即a2+a=2015,则a2+2a+b可化为a2+a+a+b=2015+a+b,然后利用根与系数的关系得到a+b=-1,再利用整体代入的方法计算即可.
解答:解:∵a,b是方程x2+x-2015=0的两个实数根,
∴a2+a-2015=0,a+b=-1,
∴a2+a=2015,
∴a2+2a+b=a2+a+a+b=2015-1=2014.
∴a2+a-2015=0,a+b=-1,
∴a2+a=2015,
∴a2+2a+b=a2+a+a+b=2015-1=2014.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
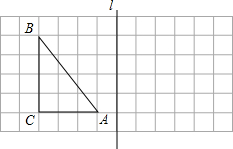 如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应),连接AA1,BB1,并计算梯形AA1B1B的面积.
如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应),连接AA1,BB1,并计算梯形AA1B1B的面积.