题目内容
解下列方程:
(1)3(x+2)2=x(x+2);
(2)x2-4x+1=0(用配方法).
(1)3(x+2)2=x(x+2);
(2)x2-4x+1=0(用配方法).
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:计算题
分析:(1)先移项得到3(x+2)2-x(x+2)=0,然后利用因式分解法解方程;
(2)利用配方法得到(x-2)2=3,然后利用直接开平方法解方程.
(2)利用配方法得到(x-2)2=3,然后利用直接开平方法解方程.
解答:解:(1)3(x+2)2-x(x+2)=0,
(x+2)(3x+6-x)=0,
x+2=0或3x+6-x=0,
所以x1=-2,x2=-3;
(2)x2-4x=-1,
x2-4x+4=3,
(x-2)2=3,
x-2=±
,
所以x1=2+
,x2=2-
.
(x+2)(3x+6-x)=0,
x+2=0或3x+6-x=0,
所以x1=-2,x2=-3;
(2)x2-4x=-1,
x2-4x+4=3,
(x-2)2=3,
x-2=±
| 3 |
所以x1=2+
| 3 |
| 3 |
点评:本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
相关题目
 如图是在方格纸上画出的一个零件图形的一半,请你以过点M,N的直线为对称轴画出另一半.
如图是在方格纸上画出的一个零件图形的一半,请你以过点M,N的直线为对称轴画出另一半.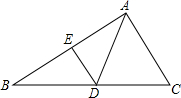 如图,△ABC中,AD=DB,∠EDB=∠DAC,求证:△ABC∽△EAD.
如图,△ABC中,AD=DB,∠EDB=∠DAC,求证:△ABC∽△EAD. 如图,某中学有一道长为35米的墙,计划用60米长的围栏靠墙围成一个面积为400平方米的矩形草坪ABCD,求该矩形草坪BC边的长.
如图,某中学有一道长为35米的墙,计划用60米长的围栏靠墙围成一个面积为400平方米的矩形草坪ABCD,求该矩形草坪BC边的长.