题目内容
(1)已知4×2a×2a+1=29,且2a+b=8,求ab的值.
(2)已知x+
=3,求x2+
,x4+
的值.
(2)已知x+
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x4 |
考点:同底数幂的乘法,完全平方公式
专题:
分析:(1)根据同底数幂的乘法法则求可得2a+3=9,求出a、b的值,然后代入求解;
(2)将x+
=3进行平方即可求解,同理求出x4+
的值.
(2)将x+
| 1 |
| x |
| 1 |
| x4 |
解答:解:(1)由题意得,2a+3=9,
解得:a=3,
则b=8-2a=8-6=2,
ab=9;
(2)∵x+
=3,
∴平方得:x2+
=9-2=7,
同理可得,x4+
=49-2=47.
解得:a=3,
则b=8-2a=8-6=2,
ab=9;
(2)∵x+
| 1 |
| x |
∴平方得:x2+
| 1 |
| x2 |
同理可得,x4+
| 1 |
| x4 |
点评:本题考查了同底数幂的乘法和完全平方公式的运用,掌握运算法则是解答本题的关键.

练习册系列答案
相关题目
双曲线y=-
上两点为(x1,y1),(x2,y2),且x1<x2<0,则下列说法正确的是( )
| 2 |
| 3x |
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、不能确定 |
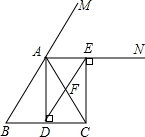 已知:如图,在△ABC中,AB=AC,AD是BC边的中线,AN为△ABC的外角∠CAM的平分线,CE⊥AN于点E,线段DE交AC于点F.
已知:如图,在△ABC中,AB=AC,AD是BC边的中线,AN为△ABC的外角∠CAM的平分线,CE⊥AN于点E,线段DE交AC于点F. 如图是在方格纸上画出的一个零件图形的一半,请你以过点M,N的直线为对称轴画出另一半.
如图是在方格纸上画出的一个零件图形的一半,请你以过点M,N的直线为对称轴画出另一半.