题目内容
5.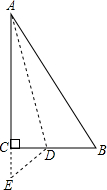 如右图,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=5cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为1cm.
如右图,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=5cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为1cm.
分析 根据勾股定理求出AB的长,根据翻折的性质可知AE=AB,根据CE=AE-AC求出CE的长即可.
解答 解:∵∠C=90°,AC=12cm,BC=5cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
由题意得,AE=AB=13,
∴CE=AE-AC=1cm.
故答案为:1.
点评 本题考查的是翻折变换,理解翻折变换的性质是解题的关键,翻折后的图形与原图形是全等的.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
15.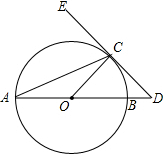 如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
 如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )
如图,AB⊙O的直径,ED切⊙O于点C,交AB的延长线于点D,且CO=CD,则∠ECA=( )| A. | 30° | B. | 45° | C. | 60° | D. | 67.5° |
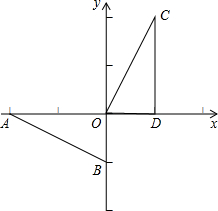 如图,在直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴的负半轴、y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.
如图,在直角坐标系中,Rt△AOB的两条直角边OA、OB分别在x轴的负半轴、y轴的负半轴上,且OA=2,OB=1.将Rt△AOB绕点O按顺时针方向旋转90°,再把所得的像沿x轴正方向平移1个单位,得△CDO.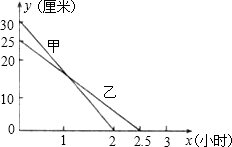 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题: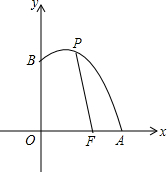 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:
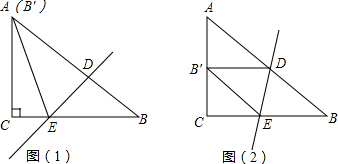
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论: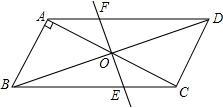 已知,如图?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F
已知,如图?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F