题目内容
13.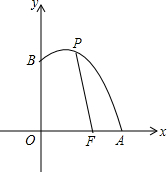 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,P是此图象上的一动点.设P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}x$(0≤x≤5),给出以下四个结论:①AF=2;②BF=5;③OA=5;④OB=4
其中正确结论的序号是①②③④.
分析 设P的坐标是(x,y),过P作PM⊥x轴于M点,在直角△PFM中,根据勾股定理,即可求得函数的解析式.根据解析式即可判断.
解答 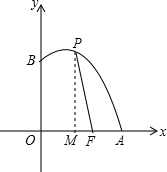 解:过P作PM⊥x轴于点M,如图所示:
解:过P作PM⊥x轴于点M,如图所示:
设P的坐标是(x,y).直角△PMF中,PM=y,MF=3-x.PM2+MF2=PF2.
则(3-x)2+y2=(5-$\frac{3}{5}$x)2.
解得:y2=-$\frac{16}{25}$x2+16.
在上式中,令y=0,解得:x=5,即OA=5,则AF=OA-OF=5-3=2,故①,③正确;
在上式中,令x=0,解得y=4.即OB=4.故④正确;
在直角△OBF中,根据勾股定理即可求得:BF=5,故②正确.
综上,正确的序号有①②③④.
故答案为:①②③④.
点评 本题考查了解直角三角形的应用中的方向角问题,是一道函数与三角形相结合的综合题,在图形中渗透运动的观点是中考中经常出现的问题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
8.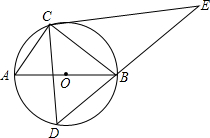 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | 5 | B. | 8 | C. | $\frac{32}{5}$ | D. | $\frac{20}{3}$ |
2.今年南方某地发生地震,政府为了尽快搭建板房安置灾民,给某厂下达了生产A种板材480002和B种板材24000m2任务.
(1)如果该厂安排210人生产这两种材,每人每天能生产A种板材60m2或B种板材40m2,请问:应分别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
(2)某灾民安置点计划用该厂上述下达任务生产的两种板材搭建甲、乙两种规格的板房共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
问:这400间板房的搭建共有多少种方案?这些方案中能最多地安置灾民的是哪一种?最多能安置灾民多少人?
(1)如果该厂安排210人生产这两种材,每人每天能生产A种板材60m2或B种板材40m2,请问:应分别安排多少人生产A种板材和B种板材,才能确保同时完成各自的生产任务?
(2)某灾民安置点计划用该厂上述下达任务生产的两种板材搭建甲、乙两种规格的板房共400间,已知建设一间甲型板房和一间乙型板房所需板材及安置人数如下表所示:
| 板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
| 甲型 | 108 | 61 | 12 |
| 乙型 | 156 | 51 | 10 |
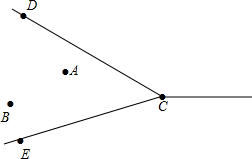 A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件:
A、B两村坐落在两条相交公路CD、CE内,现计划修建一所小学校,要求学校必须满足下列条件:
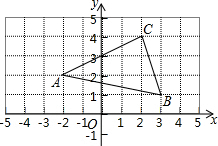 如图,在平面直角坐标系中,△ABC的各个顶点都在正方形网格的格点上,把△ABC绕点O逆时针旋转180°,得到△AB′C′,则点C′的坐标是(-2,-4).
如图,在平面直角坐标系中,△ABC的各个顶点都在正方形网格的格点上,把△ABC绕点O逆时针旋转180°,得到△AB′C′,则点C′的坐标是(-2,-4).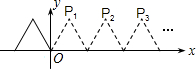 如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).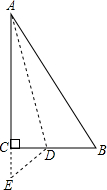 如右图,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=5cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为1cm.
如右图,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=5cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为1cm.