题目内容
15．
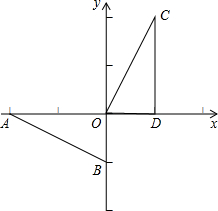如图，在直角坐标系中，Rt△AOB的两条直角边OA、OB分别在x轴的负半轴、y轴的负半轴上，且OA=2，OB=1．将Rt△AOB绕点O按顺时针方向旋转90°，再把所得的像沿x轴正方向平移1个单位，得△CDO．（1）写出点A、B、C、D的坐标；
（2）求点A和点C之间的距离．
分析 （1）根据平面直角坐标系中点的位置，可得 A，B，根据旋转平移，可得点C、D的坐标；
（2）根据勾股定理，可得AC的长．
解答 解：（1）由图，得
A（-2，0），B（0，-1），C（1，2），D（1，0）；
（2）连接AC
，
在RtACD中，由勾股定理，得
AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$．
点评 本题考查了坐标与图形变化，利用了图形的旋转、平移：不改变图形的大小形状，勾股定理．
练习册系列答案
小学教材完全解读系列答案
相关题目
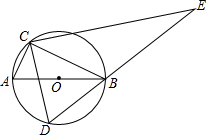如图，AB是⊙O的直径，点C在⊙O上，且tan∠ABC=$\frac{1}{2}$，D是⊙O上的一个动点（C，D两点位于直径AB的两侧），连接CD，过点C作CE⊥CD交DB的延长线于点E．若AB=2$\sqrt{5}$，则AC=2，线段CE长度的最大值是4$\sqrt{5}$．
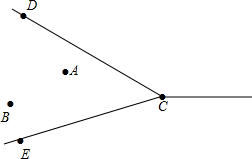A、B两村坐落在两条相交公路CD、CE内，现计划修建一所小学校，要求学校必须满足下列条件：
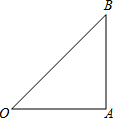如图，Rt△ABC中，∠OAB=90°，OA=AB=2，
如图，已知△ABC．
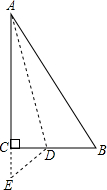如右图，有一块直角三角形纸片，∠C=90°，AC=12cm，BC=5cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为1cm．