题目内容
16.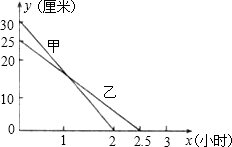 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图所示,请根据图象所提供的信息解答下列问题:(1)甲、乙两根蜡烛燃烧前的高度分别是30厘米、25厘米,从点燃到燃尽所用的时间分别是2小时、2.5小时.
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间时,甲、乙两根蜡烛的高度相差1厘米?
分析 (1)通过观察图象可以甲、乙两根蜡烛燃烧前的高度分别为30厘米,25厘米,所用的时间分别是2小时和2.5小时;
(2)运用待定系数法就可以求出甲、乙两根蜡烛燃烧时y与x之间的函数关系式,
(3)再由解析式建立方程,求出其解就可以得出高度相差1厘米时的时间.
解答 解:(1)由图象得出:
甲、乙两根蜡烛燃烧前的高度分别30cm,25cm,
从点燃到燃尽所用的时间分别是2小时,2.5小时,
故答案为:30cm,25cm;2小时,2.5小时;
(2)设y甲=k1x+b1,y乙=k2x+b2,由图象得:
$\left\{\begin{array}{l}{2{k}_{1}+{b}_{1}=0}\\{{b}_{1}=30}\end{array}\right.$,$\left\{\begin{array}{l}{2.5{k}_{2}+{b}_{2}=0}\\{{b}_{2}=25}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-15}\\{{b}_{1}=30}\end{array}\right.$,$\left\{\begin{array}{l}{{k}_{2}=-10}\\{{b}_{2}=25}\end{array}\right.$,
∴y甲=-15x+30,y乙=-10x+25;
(3)当-15x+30-(-10x+25)=1时,x=$\frac{4}{5}$,
当-10x+25-(-15x+30)=1时,x=$\frac{6}{5}$.
点评 本题考查了一次函数的应用及根据图象信息解答数学问题的能力,待定系数法求一次函数的解析式的运用,解答时根据函数的图象求出函数的解析式是关键.

练习册系列答案
相关题目
7.在平面直角坐标系中,已知点A(-4,0),B(0,3),对△AOB连续作图所示的旋转变换,依次得到三角形(1),(2),(3),(4)…,那么第(2013)个三角形的直角顶点坐标是(8052,0)

8.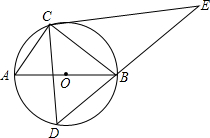 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
 如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )
如图,定点C、动点D在⊙O上,并且位于直径AB的两侧,AB=5,AC=3,过点C在作CE⊥CD交DB的延长线于点E,则线段CE长度的最大值为( )| A. | 5 | B. | 8 | C. | $\frac{32}{5}$ | D. | $\frac{20}{3}$ |
6.在tan45°,sin60°,3.14,π,0.101001,$\frac{22}{7}$中,无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
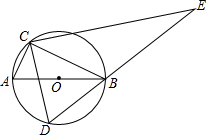 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若AB=2$\sqrt{5}$,则AC=2,线段CE长度的最大值是4$\sqrt{5}$.
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若AB=2$\sqrt{5}$,则AC=2,线段CE长度的最大值是4$\sqrt{5}$.
 如图,把△ABC绕B点逆时针方向旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC=77°.
如图,把△ABC绕B点逆时针方向旋转26°得到△A′BC′,若A′C′正好经过A点,则∠BAC=77°.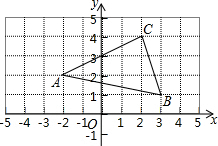 如图,在平面直角坐标系中,△ABC的各个顶点都在正方形网格的格点上,把△ABC绕点O逆时针旋转180°,得到△AB′C′,则点C′的坐标是(-2,-4).
如图,在平面直角坐标系中,△ABC的各个顶点都在正方形网格的格点上,把△ABC绕点O逆时针旋转180°,得到△AB′C′,则点C′的坐标是(-2,-4).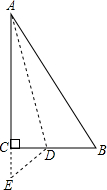 如右图,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=5cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为1cm.
如右图,有一块直角三角形纸片,∠C=90°,AC=12cm,BC=5cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为1cm.