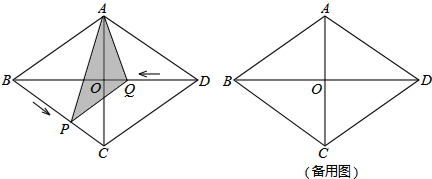
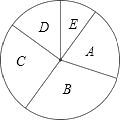
题目内容
 小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次指针指向的数字之差(第一次数字减第二次的数字)大于或等于2,小明获胜,否则小亮获胜(指针恰好指在等分线上时重新转动转盤).
小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次指针指向的数字之差(第一次数字减第二次的数字)大于或等于2,小明获胜,否则小亮获胜(指针恰好指在等分线上时重新转动转盤).(1)分别求出小明和小亮得分的概率;
(2)你认为游戏是否公平?若公平,请说明理由.
考点:游戏公平性,列表法与树状图法
专题:
分析:(1)先根据已知列表,再根据概率公式分别求出小明和小亮得分的概率即可;
(2)根据(1)求出的概率,比较出小明和小亮得分的概率大小,即可判断出是否公平.
(2)根据(1)求出的概率,比较出小明和小亮得分的概率大小,即可判断出是否公平.
解答:解:(1)依题意列表如下:
故所有等可能结果有12种,其中数字之差大于等于2的结果有3种,其它结果有9种,
则p(小明的概率)=
=
,则p(小明的概率)=
=
,
(2)这个游戏规则不公平,
∵
<
,
∴小亮获胜的概率大.
| 第二次 | 1 | 2 | 3 | 4 |
| 1 | 0 | 1 | 2 | 3 |
| 2 | -1 | 0 | 1 | 2 |
| 3 | -2 | -1 | 0 | 1 |
| 4 | -3 | -2 | -1 | 0 |
则p(小明的概率)=
| 3 |
| 12 |
| 1 |
| 4 |
| 9 |
| 12 |
| 3 |
| 4 |
(2)这个游戏规则不公平,
∵
| 1 |
| 4 |
| 3 |
| 4 |
∴小亮获胜的概率大.
点评:此题考查了游戏公平性,用到的知识点是概率公式,关键是根据概率公式比较出小明和小亮得分的概率.

练习册系列答案
相关题目
要比较两名同学在五次数学测试中谁的成绩比较稳定,应选用的统计量是( )
| A、方差 | B、中位数 |
| C、众数 | D、平均数 |
 我市某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1,(单位:cm)
我市某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1,(单位:cm)
 2011年,在长沙创建全国文明城市过程中,某学校数学兴趣小组对全校1500名学生中的部分学生进行了“垃圾分类知识”的抽样测试调查,测试问卷采用等级计分.该兴趣小组把收集到的数据统计成以下表格.
2011年,在长沙创建全国文明城市过程中,某学校数学兴趣小组对全校1500名学生中的部分学生进行了“垃圾分类知识”的抽样测试调查,测试问卷采用等级计分.该兴趣小组把收集到的数据统计成以下表格.