题目内容
12．
已知：如图，AB∥CD，CE∥BF．求证：∠C+∠B=180°．
分析 根据两直线平行，内错角相等可得∠C=∠CDB，再根据两直线平行，同旁内角互补证明．
解答 证明：∵AB∥CD，CE∥BF，
∴∠CDB+∠B=180°，
∠C=∠CDB，
∴∠C+∠B=180°．
点评 本题考查了平行线的性质，是基础题，熟记性质是解题的关键．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
在△ABC中，AB=AC，∠BAC=120°，AD⊥BC，垂足为G，且AD=AB．∠EDF=60°，其两边分别交边AB，AC于点E，F．
如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，
20．下列条件中，不能判断四边形ABCD是平行四边形的是（ ）
| A． | AB∥CD，AD∥BC | B． | AB=CD，AD∥BC | C． | AB∥CD，AB=CD | D． | ∠A=∠C，∠B=∠D |
7．
如图，四边形ABCD中，AB∥CD，对角线AC平分∠BAD．点E在AB边上，且CE∥AD．
（1）求证：四边形AECD是菱形；
（2）如果点E是AB的中点，AC=8，EC=5，求四边形ABCD的面积．
如图，四边形ABCD中，AB∥CD，对角线AC平分∠BAD．点E在AB边上，且CE∥AD．（1）求证：四边形AECD是菱形；
（2）如果点E是AB的中点，AC=8，EC=5，求四边形ABCD的面积．
4．
如图，在△ABC中，D为AB的中点，CE=3BE，CF=2AF，四边形CEDF的面积为17，则△ABC的面积为（ ）
如图，在△ABC中，D为AB的中点，CE=3BE，CF=2AF，四边形CEDF的面积为17，则△ABC的面积为（ ）| A． | 22 | B． | 23 | C． | 24 | D． | 25 |
11．
如图，为测量池塘岸边A、B两点之间的距离，小亮在池塘的一侧选取一点O，测得OA、OB的中点D、E之间的距离是14米，则A、B两点之间的距离是（ ）
如图，为测量池塘岸边A、B两点之间的距离，小亮在池塘的一侧选取一点O，测得OA、OB的中点D、E之间的距离是14米，则A、B两点之间的距离是（ ）| A． | 18 米 | B． | 24米 | C． | 28米 | D． | 30米 |
8．
如图，AB⊥CD于D，DE⊥DF，若∠BDE=60°，则∠CDF等于（ ）
如图，AB⊥CD于D，DE⊥DF，若∠BDE=60°，则∠CDF等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 120° |
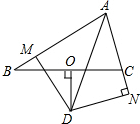在三角形ABC中∠BAC的角平分线与BC的垂直平分线相交于D点，DN⊥AC，DM⊥AB，