题目内容
7. 如图,四边形ABCD中,AB∥CD,对角线AC平分∠BAD.点E在AB边上,且CE∥AD.
如图,四边形ABCD中,AB∥CD,对角线AC平分∠BAD.点E在AB边上,且CE∥AD.(1)求证:四边形AECD是菱形;
(2)如果点E是AB的中点,AC=8,EC=5,求四边形ABCD的面积.
分析 (1)由“邻边相等的平行四边形为菱形”进行证明;
(2)根据菱形的性质和等腰三角形的性质推知△ABC是直角三角形,所以结合直角三角形的面积求法和图形得到:四边形ABCD的面积=S△AEC+S△EBC+S△ACD.
解答 (1)证明:∵AB∥CD,CE∥AD,
∴四边形AECD是平行四边形,
∵AC平分∠BAD,
∴∠EAC=∠DAC,
∵AB∥CD,
∴∠EAC=∠ACD,
∴∠DAC=∠ACD,
∴AD=CD,
∴四边形AECD是菱形;
(2)解:∵四边形AECD是菱形,
∴AE=CE,
∴∠EAC=∠ACE,
∵点E是AB的中点,
∴AE=BE,
∴∠B=∠ECB,
∴∠ACE+∠ECB=90°,即∠ACB=90°;
∵点E是AB的中点,EC=5,
∴AB=2EC=10,
∴BC=6.
∴S△ABC=$\frac{1}{2}$BC•AC=24.
∵点E是AB的中点,四边形AECD是菱形,
∴S△AEC=S△EBC=S△ACD=12.
∴四边形ABCD的面积=S△AEC+S△EBC+S△ACD=36.
点评 本题考查了菱形的判定与性质.解答(2)题时,利用了菱形的性质、直角三角形的判定等知识点,借用了“分割法”求得四边形ABCD的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
 在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )
在四边形ABCD中,AC=BD=8,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2的值为( )| A. | 64 | B. | 18 | C. | 36 | D. | 48 |
3.有甲、乙、丙三个村庄分别位于等边△ABC的顶点,在城中村改造时,为保护环境,改善居民的生活条件,政府决定铺设能够连结这三个村庄的天然气管道.设计人员给出了如图四个设计方案(点D为BC边的中点,点O为△ABC的中心,实线表示天然气管道),其中天然气管道总长最短的是( )
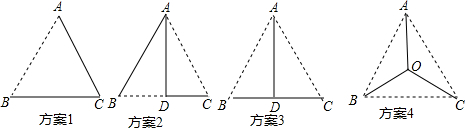

| A. | 方案1 | B. | 方案2 | C. | 方案3 | D. | 方案4 |
4.因式分解4+a2-4a正确的是( )
| A. | 4(1-a)+a2 | B. | (2-a)2 | C. | (2+a)(2-a) | D. | (2+a)2 |
 已知:如图,在?ABCD中,AC⊥AB,点E在AD的延长线上,且BE=BC.若AC=4,CE=$4\sqrt{5}$,求?ABCD的周长.
已知:如图,在?ABCD中,AC⊥AB,点E在AD的延长线上,且BE=BC.若AC=4,CE=$4\sqrt{5}$,求?ABCD的周长. 《孙子算经》是中国古代重要的数学著作,约成书于一千五百年前,共三卷,卷上叙述算筹记数的纵横相间制度和筹算乘除法,记有许多有趣的问题.其中记载:“今有木,不知长短,引绳度之,余绳四尺无寸;屈绳量之,不足一尺.木长几何?”
《孙子算经》是中国古代重要的数学著作,约成书于一千五百年前,共三卷,卷上叙述算筹记数的纵横相间制度和筹算乘除法,记有许多有趣的问题.其中记载:“今有木,不知长短,引绳度之,余绳四尺无寸;屈绳量之,不足一尺.木长几何?” 已知:如图,AB∥CD,CE∥BF.求证:∠C+∠B=180°.
已知:如图,AB∥CD,CE∥BF.求证:∠C+∠B=180°.