题目内容
9.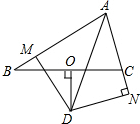 在三角形ABC中∠BAC的角平分线与BC的垂直平分线相交于D点,DN⊥AC,DM⊥AB,
在三角形ABC中∠BAC的角平分线与BC的垂直平分线相交于D点,DN⊥AC,DM⊥AB,(1)求证:BM=CN.
(2)如果AB=12cm,AC=8cm,则求线段AM的长.
分析 (1)连接DB、DC,求出DB=DC,DM=DN,根据HL证出Rt△DMB≌Rt△DNC即可;
(2)根据全等三角形的性质得到AM=AN,等量代换即可得到结论.
解答 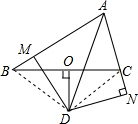 (1)证明:连接DB、DC,
(1)证明:连接DB、DC,
∵OD是BC的垂直平分线,
∴BD=CD,
∵AD平分∠BAC,DM⊥AB,DN⊥AC,
∴DM=DN,∠DMB=∠N=90°,
在Rt△DMB和Rt△DNC中
$\left\{\begin{array}{l}{DB=DC}\\{DM=DN}\end{array}\right.$
∴Rt△DMB≌Rt△DNC(HL),
∴BM=CN;
(2)在Rt△AMD和Rt△ACN中,$\left\{\begin{array}{l}{DM=DN}\\{AD=AD}\end{array}\right.$,
∴Rt△AMD≌Rt△ACN,
∴AM=AN,
∴AM=AB-CN=AB-(AM-AC),
∴AM=10.
点评 本题考查了全等三角形的性质和判定,垂直平分线性质,角平分线性质的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
4.因式分解4+a2-4a正确的是( )
| A. | 4(1-a)+a2 | B. | (2-a)2 | C. | (2+a)(2-a) | D. | (2+a)2 |
14. 如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
 如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )
如图,△ABC中,边BC=12,高AD=6.矩形MNPQ的边在BC上,顶点P在AB上,顶点N在AC上,若S矩形MNPQ=y,PN=x,则y与x的关系式为( )| A. | y=6-$\frac{1}{2}$x(0<x<12) | B. | y=-$\frac{1}{2}$x2+6x(0<x<12) | ||
| C. | y=2x2-12x(0<x<12) | D. | y=$\frac{1}{2}$x2+6x(0<x<12) |
1.下列说法:(1)矩形的对角线互相垂直且平分;(2)菱形的四边相等;(3)一组对边平行,另一组对边相等的四边形是平行四边形;(4)正方形的对角线相等,并且互相垂直平分.
其中正确的个数是( )
其中正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.下列说法正确的是( )
| A. | 三角形可以分为等边三角形、直角三角形、钝角三角形 | |
| B. | 如果一个三角形的一个外角大于与它相邻的内角,则这个三角形为锐角三角形 | |
| C. | 各边都相等的多边形是正多边形 | |
| D. | 五边形有五条对角线 |
 已知:如图,AB∥CD,CE∥BF.求证:∠C+∠B=180°.
已知:如图,AB∥CD,CE∥BF.求证:∠C+∠B=180°. 将∠B,∠E按如图所示的方式放置.请你从下列三项:①∠B=∠E;②AB∥DE;③BC∥EF中选择两项作为条件,填入“已知”栏中,另一项作为结论,填入“求证”栏中,并证明.
将∠B,∠E按如图所示的方式放置.请你从下列三项:①∠B=∠E;②AB∥DE;③BC∥EF中选择两项作为条件,填入“已知”栏中,另一项作为结论,填入“求证”栏中,并证明.


