题目内容
如图所示,已知AB∥CD,分别探究下面图形中∠APC,∠PAB,∠PCD的关系,请你在所得到的关系中,从(1)、(2)中和(3)、(4)中各选一个加以说明.结论:
(1) ;
(2) ;
(3) ;
(4) ;
证明一:我选择的是 ;
证明二:我选择的是 ;

(1)
(2)
(3)
(4)
证明一:我选择的是
证明二:我选择的是

考点:平行线的性质
专题:
分析:(1)过点P作PE∥AB,则AB∥PE∥CD,根据平行线的性质得出∠1+∠PAB=180°,∠2+∠PCD=180°,即可得出答案;
(3)根据平行线的性质得出∠PEB=∠PCD,根据三角形的外角性质得出∠PEB=∠PAB+∠APC,代入求出即可.
(3)根据平行线的性质得出∠PEB=∠PCD,根据三角形的外角性质得出∠PEB=∠PAB+∠APC,代入求出即可.
解答: 解:(1)∠APC+∠PAB+∠PCD=360°
解:(1)∠APC+∠PAB+∠PCD=360°
(2)∠APC=∠PAB+∠PCD
(3)∠PCD=∠APC+∠PAB
(4)∠PAB=∠APC+∠PCD
选(1)
(1)过点P作PE∥AB,则AB∥PE∥CD,
∴∠1+∠PAB=180°,
∠2+∠PCD=180°,
∴∠APC+∠PAB+∠PCD=360°;
(2)过点P作直线l∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB=∠3,∠PCD=∠4,
∴∠APC=∠PAB+∠PCD;
(3)∵AB∥CD,
∴∠PEB=∠PCD,
∵∠PEB是△APE的外角,
∴∠PEB=∠PAB+∠APC,
∴∠PCD=∠APC+∠PAB;
(4)∵AB∥CD,
∴∠PAB=∠PFD,
∵∠PFD是△CPF的外角,
∴∠PCD+∠APC=∠PFD,
∴∠PAB=∠APC+∠PCD.②选择结论(1),证明同;
故答案为:∠APC+∠PAB+∠PCD=360°,∠APC=∠PAB+∠PCD,∠PCD=∠APC+∠PAB,∠PAB=∠APC+∠PCD,(1),(3)
 解:(1)∠APC+∠PAB+∠PCD=360°
解:(1)∠APC+∠PAB+∠PCD=360° (2)∠APC=∠PAB+∠PCD
(3)∠PCD=∠APC+∠PAB
(4)∠PAB=∠APC+∠PCD
选(1)
(1)过点P作PE∥AB,则AB∥PE∥CD,
∴∠1+∠PAB=180°,
∠2+∠PCD=180°,
∴∠APC+∠PAB+∠PCD=360°;
(2)过点P作直线l∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB=∠3,∠PCD=∠4,
∴∠APC=∠PAB+∠PCD;
(3)∵AB∥CD,
∴∠PEB=∠PCD,
∵∠PEB是△APE的外角,
∴∠PEB=∠PAB+∠APC,
∴∠PCD=∠APC+∠PAB;
(4)∵AB∥CD,
∴∠PAB=∠PFD,
∵∠PFD是△CPF的外角,
∴∠PCD+∠APC=∠PFD,
∴∠PAB=∠APC+∠PCD.②选择结论(1),证明同;
故答案为:∠APC+∠PAB+∠PCD=360°,∠APC=∠PAB+∠PCD,∠PCD=∠APC+∠PAB,∠PAB=∠APC+∠PCD,(1),(3)
点评:本题考查了平行线的性质和三角形的外角性质的应用,主要考查学生运用平行线的性质进行推理的能力,注意:要掌握辅助线的做法.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 已知抛物线y=-x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?( )
已知抛物线y=-x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?( )| A、始终不相似 |
| B、始终相似 |
| C、只有AB=AD时相似 |
| D、无法确定 |
 如图,一次函数y=x+
如图,一次函数y=x+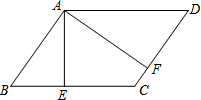 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F.
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是边AB上一点,联结CD,把△ACD沿CD所在的直线翻折,点A落在点E的位置,如果DE∥BC,那么AD的长为
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是边AB上一点,联结CD,把△ACD沿CD所在的直线翻折,点A落在点E的位置,如果DE∥BC,那么AD的长为